Рассмотренные выше методы определения спектральной функции временного ряда являются непараметрическими. Параметрический спектральный анализ подразумевает построение математической модели временного ряда и только после этого на основе найденных моделей позволяет оценить его спектральные характеристики. Математическая модель, построенная в рамках параметрического спектрального анализа, не должна точно описывать временной ряд, по которому она была восстановлена. Речь идет о совпадении вероятностных характеристик исходного ряда и модели. При таком подходе спектр является функцией параметров восстанавливаемой модели.
Использование параметрических моделей позволяет получить более точные, с более высоким разрешением спектральные оценки, чем это возможно с помощью непараметрического анализа. Параметрический анализ наиболее эффективен при работе с данными малой длины, когда непараметрические методы не могут обеспечить необходимое спектральное разрешение.
Наибольшее распространение получил подход, основанный на
построении линейных стационарных моделей. В соответствии с этим
подходом анализируемый процесс рассматривается как процесс на
выходе линейной системы, на вход которой поступает белый шум.
Поскольку белый шум имеет равномерную спектральную плотность, то,
пропуская его через линейную систему бесконечной размерности
(или, что то же самое, через бесконечное число линейных систем,
соединенных последовательно или параллельно), можно получить
спектральную плотность мощности любой формы. Поэтому линейная
модель пригодна для аппроксимации многих встречающихся на практике
детерминированных и случайных процессов с дискретным временем.
Спектральная характеристика линейных моделей полностью определяется
параметрами модели и дисперсией белого шума
![]() .
.
Весь класс линейных моделей может быть представлен в виде:
Здесь ![]() -- анализируемый процесс c периодом
дискретизации
-- анализируемый процесс c периодом
дискретизации ![]() ,
, ![]() -- белый шум с
нулевым средним значением
-- белый шум с
нулевым средним значением
![]() и корреляционной
функцией
и корреляционной
функцией
![]() (см.
Приложение). Спектральная плотность белого шума
(см.
Приложение). Спектральная плотность белого шума
![]() принимает постоянное значение для всех частот, равное дисперсии:
принимает постоянное значение для всех частот, равное дисперсии:
![]() . Если все коэффициенты
. Если все коэффициенты ![]() второго слагаемого равны нулю (кроме
второго слагаемого равны нулю (кроме ![]() ,
, ![]() ), то получается так
называемая модель авторегрессии (АР), т.е. модель процесса,
значение которого в момент времени
), то получается так
называемая модель авторегрессии (АР), т.е. модель процесса,
значение которого в момент времени ![]() формируется как комбинация
значений этого процесса в предшествующие моменты времени
формируется как комбинация
значений этого процесса в предшествующие моменты времени
![]() и значения независимой случайной составляющей
и значения независимой случайной составляющей ![]() . Если
равны нулю все коэффициенты
. Если
равны нулю все коэффициенты ![]() , то модель называется моделью
скользящего среднего (СС) и описывает безинерционное (не
зависящее от предыдущих моментов времени) преобразование случайного
процесса. Целые положительные числа
, то модель называется моделью
скользящего среднего (СС) и описывает безинерционное (не
зависящее от предыдущих моментов времени) преобразование случайного
процесса. Целые положительные числа ![]() и
и ![]() задают порядок
моделей АР(
задают порядок
моделей АР(![]() ) и CC(
) и CC(![]() ), соответственно. Когда
), соответственно. Когда ![]() и
и ![]() отличны
от нуля, получается комбинированная модель --
авторегрессии - скользящего среднего АРСС(
отличны
от нуля, получается комбинированная модель --
авторегрессии - скользящего среднего АРСС(![]() ). Выбор типа модели
предшествует спектральному анализу и делается на основе сведений о
физической природе анализируемого случайного процесса. Кроме того, для
выбора модели требуются предварительные сведения о возможной форме
спектральной плотности мощности. Если исследуемый сигнал по
предположению имеет спектр с острыми пиками, но без глубоких впадин
(нулей), то наиболее подходящей является АР-модель, поскольку она дает
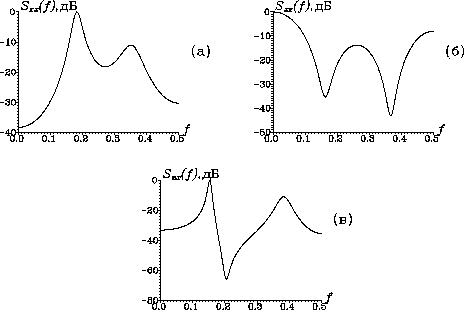
спектр с резкими всплесками на отдельных частотах (рис. 15, а).
Если, наоборот, предполагаемый спектр имеет глубокие нули, но не
характеризуется острыми пиками, то подойдет СС-модель (рис. 15,
б). АРСС-модель может применяться в обоих предельных случаях
(рис. 15, в). В тех случаях, когда одинаково пригодны несколько
моделей, следует использовать ту из них, которая имеет наименьшее число
параметров или, другими словами, наименьший порядок, поскольку оценки с
хорошими статистическими свойствами можно получить, как правило,
когда число оцениваемых параметров минимально. Кроме того, выбор
модели зависит от имеющихся вычислительных ресурсов: АР-модели требуют
значительно меньше вычислительных затрат, чем СС- и АРСС-модели.
При неверном выборе модели оценка спектра будет ошибочной и,
скорее всего, будет обладать худшими свойствами, чем оценка,
полученная с помощью непараметрических методов.
). Выбор типа модели
предшествует спектральному анализу и делается на основе сведений о
физической природе анализируемого случайного процесса. Кроме того, для
выбора модели требуются предварительные сведения о возможной форме
спектральной плотности мощности. Если исследуемый сигнал по
предположению имеет спектр с острыми пиками, но без глубоких впадин
(нулей), то наиболее подходящей является АР-модель, поскольку она дает
спектр с резкими всплесками на отдельных частотах (рис. 15, а).
Если, наоборот, предполагаемый спектр имеет глубокие нули, но не
характеризуется острыми пиками, то подойдет СС-модель (рис. 15,
б). АРСС-модель может применяться в обоих предельных случаях
(рис. 15, в). В тех случаях, когда одинаково пригодны несколько
моделей, следует использовать ту из них, которая имеет наименьшее число
параметров или, другими словами, наименьший порядок, поскольку оценки с
хорошими статистическими свойствами можно получить, как правило,
когда число оцениваемых параметров минимально. Кроме того, выбор
модели зависит от имеющихся вычислительных ресурсов: АР-модели требуют
значительно меньше вычислительных затрат, чем СС- и АРСС-модели.
При неверном выборе модели оценка спектра будет ошибочной и,
скорее всего, будет обладать худшими свойствами, чем оценка,
полученная с помощью непараметрических методов.
 |
Определим связь спектра последовательности ![]() и параметров
модели (1.68). Для этого применим преобразование Фурье
(1.33) к выражению (1.68), используя свойство
(1.45):
и параметров
модели (1.68). Для этого применим преобразование Фурье
(1.33) к выражению (1.68), используя свойство
(1.45):
В результате получим следующее соотношение:
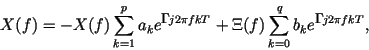
где ![]() -- преобразование Фурье белого шума.
-- преобразование Фурье белого шума.
Перегруппируем слагаемые и выразим спектральную функцию
![]() :
:
Поскольку для случайных процессов преобразование Фурье не определено,
то необходимо перейти к спектральным плотностям. На основе
соотношений (1.64) и (1.69) связь спектра
мощности ![]() линейной стационарной модели (1.68) с
параметрами модели и дисперсией белого шума запишется в виде:
линейной стационарной модели (1.68) с
параметрами модели и дисперсией белого шума запишется в виде:
Таким образом, зная параметры ![]() ,
, ![]() и величину
дисперсии шума
и величину
дисперсии шума
![]() , можно определить спектральную функцию
процесса.
, можно определить спектральную функцию
процесса.
Рассмотрим на примере авторегрессионной модели первого порядка (![]() )
алгоритм нахождения спектральной функции анализируемого
временного ряда с шагом дискретизации
)
алгоритм нахождения спектральной функции анализируемого
временного ряда с шагом дискретизации ![]() . Модель (1.68) для
. Модель (1.68) для
![]() имеет вид:
имеет вид:
В соответствии с выбранной моделью выражение (1.70)
упрощается и принимает форму:
Для того, чтобы оценить спектральную плотность ![]() , необходимо
предварительно найти оценки дисперсии шума
, необходимо
предварительно найти оценки дисперсии шума
![]() и параметра
и параметра ![]() . Определим их. С этой целью
сначала возьмем математическое ожидание от обеих частей уравнения
(1.71):
. Определим их. С этой целью
сначала возьмем математическое ожидание от обеих частей уравнения
(1.71):
Математическое ожидание в первом слагаемом правой части
(1.73) равно
![]() , поскольку для стационарных
случайных процессов математическое ожидание не зависит от начала
отсчета времени. Второе слагаемое в правой части равно нулю
вследствие того, что белый шум имеет нулевое среднее значение.
Итак, выражение (1.73) имеет вид:
, поскольку для стационарных
случайных процессов математическое ожидание не зависит от начала
отсчета времени. Второе слагаемое в правой части равно нулю
вследствие того, что белый шум имеет нулевое среднее значение.
Итак, выражение (1.73) имеет вид:
Подсчитаем теперь дисперсию от обеих частей выражения (1.71):
Учитывая, что для стационарных СП
![]() , получим
соотношение
, получим
соотношение
Далее подставим в (1.75) функцию ![]() , описываемую
формулой (1.71):
, описываемую
формулой (1.71):
Множитель, заключенный в квадратные
скобки, в соответствии с формулой (1.12) для бесконечного
ряда (
![]() ) и нулевого среднего представляет собой
дисперсию
) и нулевого среднего представляет собой
дисперсию ![]() . Второе слагаемое правой части (1.76)
равно нулю в силу статистической независимости процессов
. Второе слагаемое правой части (1.76)
равно нулю в силу статистической независимости процессов ![]() и
и ![]() . Поэтому окончательно получаем выражение:
. Поэтому окончательно получаем выражение:
Из этого соотношения следует, что параметр ![]() равен:
равен:
Следовательно, искомый
коэффициент АР-модели ![]() можно оценить по анализируемому процессу
можно оценить по анализируемому процессу
![]() конечной длины
конечной длины ![]() следующим образом:
следующим образом:
Для оценки дисперсии шума можно теперь воспользоваться выражением
(1.74) и оценкой дисперсии (1.12):
Вычисленные оценки параметра ![]() и дисперсии шума
и дисперсии шума
![]() теперь
можно
использовать для оценки спектра процесса по формуле
(1.72).
теперь
можно
использовать для оценки спектра процесса по формуле
(1.72).
Как видно из рассмотренного выше примера, вычисление параметров
авторегрессионной модели сводится к оценке моментных
функций анализируемого процесса. Точно также с помощью
моментных функций оцениваются параметры АР-моделей более высоких
порядков. Оценка параметров СС-моделей является более сложной
вычислительной процедурой, связанной с решением
экстремальной задачи методом наименьших квадратов [7]. При
вычислении параметров АРСС-модели задача еще более усложняется,
поскольку сначала надо выбрать двумерный порядок модели ![]() ,
затем найти параметры АР-части модели и, наконец, параметры,
относящиеся к СС-части. Вычислительные сложности при нахождении
параметров моделей связаны с необходимостью решения систем линейных
(а в некоторых случаях -- нелинейных) алгебраических уравнений
большой размерности. На сегодняшний день существует большое
количество статистических пакетов прикладных программ, эффективно
решающих задачу параметрического спектрального оценивания и
помогающих оценить ошибку выбора порядка модели. Однако решение
главного вопроса о выборе типа модели остается за исследователем.
,
затем найти параметры АР-части модели и, наконец, параметры,
относящиеся к СС-части. Вычислительные сложности при нахождении
параметров моделей связаны с необходимостью решения систем линейных
(а в некоторых случаях -- нелинейных) алгебраических уравнений
большой размерности. На сегодняшний день существует большое
количество статистических пакетов прикладных программ, эффективно
решающих задачу параметрического спектрального оценивания и
помогающих оценить ошибку выбора порядка модели. Однако решение
главного вопроса о выборе типа модели остается за исследователем.