П1.5 Вычисление среднего значения и дисперсии

Среднее значение и дисперсию вычислить несложно. Однако при проведении вычислений на ЭВМ иногда возникают неожиданные проблемы. Кроме того, на практике обычно неизвестна плотность вероятности $p(x)$ и, следовательно, расчет по формулам (1.5) и (1.6) невозможен. Поэтому приходится оценивать среднее значение и дисперсию по данным конечной протяженности с использованием выражений (1.7) и (1.8).

Среднее значение можно оценить простым усреднением всех значений временного ряда:

$$\begin{eqnarray*} \hat{\mu} =\frac {1}{N}\sum _{i=1}^{N}x_i. \end{eqnarray*}$$

Здесь $N$ -- количество независимых наблюдений (размер выборки).

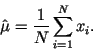
Существует другой метод оценивания среднего, который дает более точные результаты. Он состоит в вычислении частных сумм следующим образом. Пусть число данных равно степени двойки, т.е. $N=2^m$, тогда вычисления производят в $m$ стадий:

$$\begin{eqnarray*} \bar{x}_1(i)&=& \frac {1}{2} [x(2i)+x(2i+1)],~~~ i=0, \dots, \... ...\bar{x}_m(0)= \frac {1}{2} [\bar {x}_{m-1}(0)+\bar{x}_{m-1}(1)], \end{eqnarray*}$$

т.е. каждый раз последовательно складывают числа исходных данных и усредняют их. Этот метод позволяет избежать ошибки округления, если данные случайны. Когда ведутся вычисления с плавающей точкой, можно после каждой итерации заново нормировать массив, и значения данных никогда не поглотятся шумом, вызванным округлением.

Для вычисления выборочного среднего значения часто также применяют формулу:

$$\mu _k =\left( \sum _{i=0}^{k-1}x_i\right)+x_k,~~~k=0,1,\dots , N-1,~~~ \hat{\mu}=\frac {1}{N}\mu _{N-1},$$ (П11)

т.е. накапливают значения данных из последовательности. Если сумма $k$ величин оказывается существенно больше $x_k$, то ошибка округления может оказаться того же порядка, что и значение $x_k$. В этом случае применение вычислений с плавающей точкой может стать проблематичным.

Оценку дисперсии чаще всего производят по формуле

$$\hat{\sigma}^2 =\frac {1}{N-1}\sum_{i=0}^{N-1}(x_i-\hat{\mu})^2,$$ (П12)

которая является наименее чувствительной к ошибке округления.

Существует также множество других способов расчета оценок средних значений и дисперсии. Об оценках никогда нельзя определенно сказать, что они верны или неверны, поскольку на практике точное значение оцениваемого параметра неизвестно. Тем не менее, некоторые оценки можно считать хорошими или лучшими по сравнению с другими. С практической точки зрения лучшим вариантом является расчет оценок различными способами и затем проведение анализа полученных результатов.