П1.4 Среднее значение и дисперсия

Свойства реализаций стационарных СП и характерные особенности временных рядов можно изучать, рассчитывая так называемые начальные и центральные моменты. Понятие моментов вводится через математическое ожидание функции.

Определение. Математическое ожидание любой детерминированной функции $g(x_1,x_2,...,x_k)$ от $k$ случайных аргументов, обозначается $E[g(x_1,x_2,...,x_k)]$ и определяется следующим образом:

$$E[g(x_1,x_2,...,x_k)] = ~$$ (П2)

$$~ = \int_{-\infty}^{\infty}...\int_{-\infty}^{\infty} g(x_1,x_2,...,x_k)p(x_1,x_2,...,x_k)dx_1...dx_k;$$

здесь  $p(x_1,x_2,...,x_k)$ -- $k$-мерная  плотность  вероятности. Операция $E[...]$ означает усреднение по ансамблю реализаций и представляет собой интегрирование по диапазону возможных значений случайных величин с учетом вероятности получения данного значения.

Математическое ожидание (1.2) для функции одного случайного аргумента $g(x)$ определяется выражением:

$$\begin{eqnarray*} E[g(x)]=\int_{-\infty}^{\infty}g(x)p(x)dx, \end{eqnarray*}$$

в котором $p(x)$ -- одномерная плотность вероятности.

С помощью функций вида $g(x)=x^n$ вводятся начальные моменты случайной величины:

$$E[X^n]=\int_{-\infty}^{\infty}x^n p(x)dx$$ (П3)

и центральные моменты:

$$E[(X-E[X])^n]=\int_{-\infty}^{\infty}\left(x-E[X]\right)^n p(x)dx.$$ (П4)

Индекс $n$ определяет порядок моментов.

Мы рассмотрим не все моменты, а лишь некоторые из них, которые наряду с плотностью вероятности, играют важную роль при анализе временных рядов.

Первый начальный момент ( среднее значение, или математическое ожидание) $\mu$ характеризует центр рассеяния данных, а второй центральный момент ( дисперсия) $\sigma ^2$ -- величину рассеяния данных.

Определение. Пусть СП характеризуется плотностью вероятности $p(x)$, тогда средним значением случайного процесса $X(t)$ называется интеграл (в формуле (1.3) $n=1$)

$$\mu_x=E [X]= \int ^{\infty }_{-\infty } xp(x)dx.$$ (П5)

Определение. Дисперсией случайного процесса $X(t)$ называется интеграл (в формуле (1.4) $n=2$)

$$\sigma_x^2=E[(X-\mu_x)^2]= \int ^{\infty }_{-\infty } (x-\mu_x)^2p(x)dx.$$ (П6)

Для эргодических СП усреднение по ансамблю реализаций заменяется усреднением по времени наблюдения одной реализации [1]. Поэтому определения среднего значения и дисперсии для эргодических случайных процессов имеют вид:

$$\mu_x = \lim_{T\rightarrow \infty}\frac{1}{2T}\int ^{T}_{-T} x(t)dt= \langle x \rangle ,$$ (П7)

$$\sigma^2_x = \lim_{T\rightarrow \infty}\frac{1}{2T}\int ^{T}_{-T} (x(t)-\mu_x)^2 dt= \langle (x- \langle x \rangle )^2 \rangle ;$$ (П8)

здесь символ $\langle ... \rangle$ используется для обозначения усреднения по времени, $2T$ -- время наблюдения реализации СП. Индекс "$x$" у величин $\mu$ и $\sigma ^2$ обычно опускают, если ясно, о какой случайной величине идет речь. Видно (формулы (1.7) и (1.8)), что расчет $\mu$ и $\sigma ^2$ по одной реализации эргодического СП можно осуществить без знания плотности вероятности, которая на практике, как правило, неизвестна.

Параметр $\mu$ называют еще истинным средним, а величину $\sigma$, равную квадратному корню из дисперсии, -- стандартным, или среднеквадратическим отклонением. В электрических схемах дисперсия обычно соотносится со средней мощностью, выделяемой на активном сопротивлении переменной составляющей приложенного к нему напряжения или протекающего в нем тока. Среднеквадратическое отклонение соответствует показаниям вольтметра или амперметра, стрелки которых отклоняются на угол, пропорциональный эффективному значению переменной составляющей тока или напряжения, и которые не реагируют на постоянную составляющую, например, вследствие того, что на выходе прибора установлен разделительный конденсатор. Среднее значение отождествляют с постоянной составляющей напряжения или тока.

Пример. Пусть случайная величина $X$ имеет равномерную плотность вероятности (рис. 5):

$$p(x) = \left\{ \begin{array}{cc} 0, & \mbox{ $-\infty <x\le 20$,}... .../20, & \mbox{ $20<x\le 40$,} \\ 0, & \mbox{ $40<x<\infty$}. \end{array}\right.$$ (П9)

: Рис. 5. Плотность вероятности (1.9).

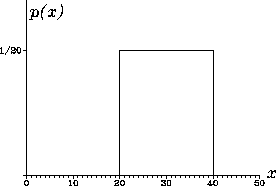Такая плотность вероятности характеризует, например, пилообразное напряжение, имеющее случайное начальное значение и изменяющееся линейно в диапазоне от $20 B$ до $40 B$. Формулы (1.5) и (1.6) дают следующие значения математического ожидания и дисперсии: $\mu = 30~B$, $\sigma^2 = 33.3~B^2$. Если измерение пилообразного напряжения выполняется при помощи вольтметра постоянного тока, то прибор должен показать $30~B$, а если при помощи вольтметра эффективных значений переменного тока, не реагирующего на постоянную составляющую, то последний покажет $\sqrt {33.3}~B$.

Введенные моменты случайной величины помогают составить наглядное представление о плотности распределения вероятностей. Чтобы показать это, рассмотрим нормальное (гауссово) распределение (рис. 6):

$$p(x)=\frac {1}{\sqrt{2\pi}\sigma}\exp\left[-(x-\mu)^2/(2\sigma ^2)\right].$$ (П10)

: Рис. 6. Плотность вероятности гауссовой случайной величины.

Нормальное распределение относится к числу наиболее распространенных и важных. На практике оно используется для описания многих явлений, которые формируются статистически независимыми процессами; пример -- распределение амплитуды дробового шума в радиоэлектронных приборах, распределение расстояний, которые пробегает броуновская частица в единицу времени.

Исследуем график нормального распределения.

1. Определим максимум функции (1.10). Видно, что плотность распределения вероятностей гауссовой случайной величины имеет один максимум, который обратно пропорционален среднеквадратическому отклонению $\sigma$; функция достигает максимума в точке $x_{max}=\mu$ (см. (1.10)). Значение $x_{max}$ характеризует положение графика функции на числовой оси. Это означает, что среднее значение $\mu$ (математическое ожидание) является параметром положения и соответствует максимуму нормальной плотности вероятности.

2. График функции имеет точки перегиба, положение которых на числовой оси можно найти, приравнивая нулю вторую производную функции (1.10) по переменной $x$. Вычисления дают следующий результат:

$$\begin{eqnarray*} p(\mu \pm \sigma)=\frac {0.607}{\sqrt{2\pi}\sigma}. \end{eqnarray*}$$

Это означает, что квадратный корень из дисперсии характеризует степень сжатия или растяжения графика плотности и является параметром масштаба. Ширина нормальной плотности вероятности прямо пропорциональна среднеквадратическому отклонению. В точках ( $\mu \pm \sigma$) производная $dp(x)/dx$ достигает своего максимального значения.

Таким образом, среднее значение (математическое ожидание) случайной величины характеризует центр нормального распределения, а корень из дисперсии -- разброс случайной величины относительно этого среднего. Функция (1.10) является двухпараметрической: нормальное распределение полностью определяется средним $\mu$ и дисперсией $\sigma$.

Все начальные моменты, в том числе и среднее значение, зависят от выбора начала отсчета $x$, т.е. они изменяются при прибавлении к случайной величине постоянного слагаемого. Центральные моменты, к которым относится дисперсия, зависят от выбранных единиц измерения. Чтобы устранить эти недостатки, моменты нормируют, в результате чего получаются безразмерные величины, не зависящие от выбора начала отсчета исходной случайной величины. Чаще всего из нормированных моментов на практике используют асимметрию $a$ (третий момент) и эксцесс $e$ (четвертый момент):

$$\begin{eqnarray*} a=\frac {E[(x-\mu)^3]}{\sigma ^{3}}, ~~~~e=\frac {E[(x-\mu)^4]}{\sigma ^4}. \end{eqnarray*}$$

Асимметрия характеризует несимметричность распределения случайной величины, а эксцесс -- степень выраженности хвостов распределения, т.е. частоту появления удаленных от среднего значений. Значения асимметрии и эксцесса используют на практике для проверки гипотезы о принадлежности данных к заданному распределению. Например, для нормального распределения асиммерия и эксцесс равны соответственно: $a=0$, $e=3\sigma ^4$. Нулевая асимметрия свидетельствует о симметричности гауссова распределения. Если эксцесс какого-либо распределения превосходит гауссов, то это указывает на значительное количество данных с большими амплитудами. Распределение с таким эксцессом имеет более толстые хвосты функции плотности, чем нормальное.