П2.9 Вычисление спектральной плотности

Основными методами оценки спектральной плотности является ее вычисление через ковариционные функции и финитное преобразование Фурье.

Для того, чтобы оценить спектральную плотность через финитное преобразование Фурье, как было указано, необходимо предусмотреть процедуру усреднения спектральной функции, вычисленной по ансамблю реализаций конечной длины. Если имеется в наличии достаточно большое число выборок случайного процесса $\{x_i(t)\}$, то процедура оценки спектра мощности состоит в вычислении преобразования Фурье $F_x(f)$ по реализации конечной длины, например, с помощью БПФ, и усреднения квадрата преобразования $F_x^2(f)$ по ансамблю выборок. Эффективность такой оценки определяется длиной выборок и их количеством.

Аналогично оценивается спектр мощности с помощью ковариационной функции: сначала производится оценка ковариационной функции для ансамбля реализаций, а затем вычисляется преобразование Фурье полученной функции.

Однако на практике вместо совокупности выборок в распоряжении исследователя имеется лишь одна временная последовательность. Посмотрим, как в этом случае можно оценить функцию спектральной плотности через ковариационные функции и финитное преобразование Фурье.

В предположении эргодичности ковариационную функцию можно определить с помощью процедуры временного усреднения по формуле (1.28). Поскольку в (1.28) временной интервал $\tau$ должен быть намного меньше интервала усреднения $T$, то величина $\tau$ меняется в пределах от $0$ до некоторого $\tau_m$. Следовательно, ковариационная функция определяется соотношением (1.28) для $\vert\tau\vert\le \tau_m$ и равна нулю для $\vert\tau\vert> \tau_m$. Другими словами, оценка ковариационной функции является произведением оценки истинной ковариационной функции и временного прямоугольного окна. Как следствие, при преобразовании Фурье возникнет эффект утечки. Это означает, что для оценки спектра мощности через ковариационные функции, также как при вычислении преобразования Фурье конечного временного ряда, необходимо использовать оконные функции. Если ковариационная функция является спадающей, т.е. не содержит периодических составляющих и равна нулю для $\vert\tau\vert> \tau_m$, то оконные функции использовать не нужно.

Подход, основанный на временном усреднении, применим только в случае вычисления спектральной плотности через ковариационные функции, но не может быть использован при оценках через финитное преобразование Фурье, поскольку последнее не зависит от времени. Поэтому при оценке спектра мощности с помощью финитного преобразования Фурье производят псевдоусредение по ансамблю. Отметим, что вычисление спектра мощности через финитное преобразование Фурье является выгодным только тогда, когда используется процедура БПФ. В этом случае затраты машинного времени резко сокращаются по сравнению с другими подходами, а статистические свойства оценки спектра обладают той же устойчивостью. Рассмотрим три наиболее широко используемых метода расчета функции спектральной плотности по одной реализации случайного процесса через финитное преобразование Фурье с помощью БПФ: метод Даньелла, метод Бартлетта и метод Уэлча. Эти методы названы по именам предложивших их исследователей. Методы Бартлетта и Уэлча относятся к так называемым периодограммным методам, в которых используется псевдоусреднение спектральных функций по ансамблю.

Метод Даньелла. Раньше было отмечено, что если применить преобразование Фурье к бесконечной реализации случайного процесса $x(t)$, то полученные коэффициенты преобразования будут иметь большую дисперсию или, другими словами, будут флуктуировать относительно среднего уровня. Даньелл предложил для сглаживания флуктуаций использовать усреднение по соседним спектральным отсчетам. При применении алгоритма БПФ для временного ряда $x(i)$ длины $N$ и с периодом дискретизации $T$ коэффициенты преобразования Фурье $X(f_k)$ будут определены на сетке частот $f_k=k/(TN)$, $0\le k\le N-1$. Оценка спектра мощности на частоте $f_i$ получается путем усреднения значений $\vert X(f_k)\vert^2$ в $m$ точках с каждой стороны от этой частоты:

$$\begin{eqnarray*} \hat{S}_{xx}(f_i)=\frac{1}{2m+1}\sum_{k=i-m}^{k=i+m} \vert X(f_k)\vert^2 . \end{eqnarray*}$$

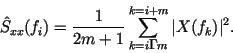
Метод Бартлетта. Сглаживание по методу Бартлетта основано на создании псевдоансамбля реализаций за счет деления временного ряда длины $N$ на $P$ неперекрывающихся сегментов, имеющих длину $M$, такую, что $MP\le N$. Тогда $p$-й сегмент будет состоять из значений:

$$\begin{eqnarray*} x^p(i)=x(pM+i),~~~0\le i \le M-1, \end{eqnarray*}$$

где индекс $p$ означает номер сегмента. Для каждого сегмента с помощью алгоритма БПФ вычисляется спектральная функция, а затем с целью получения оценки спектра мощности производится процедура усреднения спектров по ансамблю сегментов:

$$\begin{eqnarray*} \hat{S}_{xx}(f_k)=\frac{1}{P}\sum_{p=0}^{P-1}\vert X^p(f_k)\vert^2. \end{eqnarray*}$$

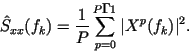
Эффективность оценки спектральной плотности по методу Бартлетта определяется числом сегментов $P$ и их длиной $M$: дисперсия (ошибка) оценки уменьшается с ростом $P$, а спектральное разрешение увеличивается с ростом $M$. Поэтому для получения оценки с меньшей дисперсией и необходимым разрешением для данной длины реализации $N$ необходимо подобрать оптимальное соотношение между $P$ и $M$. Обычно производятся расчеты для различных комбинаций $P$ и $M$, затем результаты сравниваются и выбирается оптимальная комбинация.

Метод Уэлча. Уэлч модифицировал основную схему метода сегментирования и усреднения Бартлетта путем применения оконных функций и использования перекрывающихся сегментов. Цель применения окна -- за счет незначительного ухудшения спектрального разрешения ослабить эффект утечки, а цель перекрытия сегментов -- увеличить число усредняемых сегментов и тем самым уменьшить дисперсию оценки спектра мощности. Временной ряд $x(i)$ длины $N$ разбивается на $P$ сегментов, имеющих длину $M$, причем сегменты сдвинуты друг относительно друга на величину $D$. Число сегментов определяется целой частью числа $(N-M)/D+1$. Процедура вычисления спектра мощности аналогична методу Бартлетта, за исключением того, что преобразование Фурье применяется теперь к взвешенному c помощью оконной функции $w(i)$ сегменту

$$\begin{eqnarray*} x^p(i)=w(i)x(pD+i),~~~0\le i \le M-1; \end{eqnarray*}$$

номер сегмента лежит в интервале $0\le p \le P-1$. В качестве оконной функции можно использовать любую из описанных в п.1.2.6. Выбор числа сегментов также произволен. В авторском варианте Уэлч предлагает использовать окно Ханна и $50$-процентное перекрытие сегментов. Эффективность оценки спектра мощности также, как и в методе Бартлетта, определяется величинами $P$ и $M$.

По аналогии  с описанными методами  рассчитываются взаимные спектральные плотности, с той лишь разницей, что вместо усреднения величины $\vert X(f_k)\vert^2$ производится усреднение произведения двух величин $\vert X(f_k)Y^*(f_k)\vert$   для  оценки  функции  $S_{xy}(f_k)$  и  усреднение $\vert Y(f_k)X^*(f_k)\vert$ для оценки $S_{yx}(f_k)$.