В общем случае
понятие эргодичности вводится относительно определенных статистических
характеристик [1]. Например, если понятие эргодичности
рассматривается относительно одномерной плотности вероятности, то
говорят об эргодичности первого порядка. В данном пособии
подразумевается эргодичность в строгом смысле: СП называется
эргодическим, если все его статистические характеристики можно
получить на основе знания характеристик отдельно взятой реализации
СП.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
процессаП1
Ниже будут даны свойства
ковариационной функции, из которых ясно, что ковариационная функция при
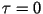 характеризует среднюю энергию процесса.
характеризует среднюю энергию процесса.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
процессаП1
В данном пособии термин cредняя
энергия используется по отношению к одной реализации СП.
Средняя энергия 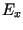 реализации
реализации 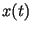 , которая имеет конечную или бесконечную длительность
, которая имеет конечную или бесконечную длительность
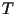 , определяется выражением:
, определяется выражением:
здесь 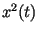 -- мгновенная энергия реализации в момент времени
-- мгновенная энергия реализации в момент времени
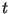 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... ФурьеП1
Примеры преобразований Фурье
некоторых других функций можно найти в [4] и [5].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... аргументП1
В
записанных выражениях для краткости вместо 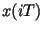 используется обозначение
используется обозначение 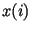 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... табл. 2П1
В табл. 2.
функция
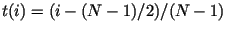 определена в
диапазоне значений
определена в
диапазоне значений
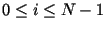 . Типичные значения параметров окна
Наттолла следующие:
. Типичные значения параметров окна
Наттолла следующие:
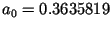 ,
, 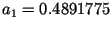 ,
, 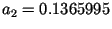 ,
,
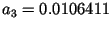 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
вейв\-лет-преобразованияП1
Преобразование Гильберта и
вейвлет-преобразование применяются также для исследования
свойств стационарных СП.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... анализаП1
Методами регрессионного анализа в общем случае решается широкий круг
задач, связанных с построением функциональных зависимостей между двумя
наборами наблюдений [9,13,14,15].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
сигналаП1
Аналитическим называется комплексный
сигнал, зависящий от действительного аргумента и равный пределу
некоторой аналитической функции при стремлении мнимой части ее
аргумента к нулю.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
БПФП1
Как правило, пакеты прикладных программ содержат
два типа алгоритмов БПФ -- действительный и комплексный.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... вейвлетомП1
wavelet -- маленькая волна (англ.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...\space П1
Строго
говоря, для рассматриваемой реализации (рис. 20, а) спектр
мощности 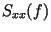 не определен, поскольку реализация нестационарна.
Поэтому на рис. 20, б показан квадрат спектральной функции
не определен, поскольку реализация нестационарна.
Поэтому на рис. 20, б показан квадрат спектральной функции
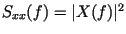 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
...
мощ\-нос\-тиП1
Определения автоковариационной
функции и спектра мощности см. в пп. 1.1.6. и 1.2.7. соответственно
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... видП1
Выражения для
автоковариационной функции и дисперсии узкополосного шума записаны в
приближении 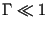 . В общем случае эти соотношения нельзя
записать через элементарные функции.
. В общем случае эти соотношения нельзя
записать через элементарные функции.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
![]() не определен, поскольку реализация нестационарна.
Поэтому на рис. 20, б показан квадрат спектральной функции
не определен, поскольку реализация нестационарна.
Поэтому на рис. 20, б показан квадрат спектральной функции
![]() .
.
![]() . В общем случае эти соотношения нельзя
записать через элементарные функции.
. В общем случае эти соотношения нельзя
записать через элементарные функции.