П1.1 Некоторые понятия теории случайных процессов.
Классификация случайных процессов

Кратко напомним основные понятия и термины, используемые в теории СП.

Пусть имеются результаты наблюдений некоторого явления на бесконечном интервале времени. Эти наблюдения нельзя описать конкретной математической зависимостью, поскольку каждое наблюдение какого-либо процесса дает невоспроизводимый результат и можно указать только вероятность получения данного результата. Поэтому говорят, что результаты образуют случайную реализацию $x(t)$. Такая реализация является лишь одной из бесконечного множества потенциально возможных. Совокупность всех реализаций образует случайный процесс $X(t) = \{x_k(t)\}$; здесь индекс $k$ меняется от нуля до бесконечности и обозначает номер реализации (эксперимента). Бесконечное множество реализаций $\{x_k(t)\}$ называется ансамблем. Именно для ансамбля реализаций, регистрируемых на бесконечном интервале времени вводятся вероятностные характеристики, определяющие свойства случайного процесса. Это означает, что СП может быть описан с помощью количественных характеристик только при наличии большого числа идентичных испытаний.

: Рис. 1. Классификация случайных процессов.

Результат исхода испытания $x_k(t_i)$ для любой реализации и в любой фиксированный момент времени $t_i$ представляет собой значение случайной величины $X(t_i)$. Реализации СП и ансамбль реализаций являются множеством случайных величин. Поэтому вероятностное описание случайных величин служит одновременно вероятностным описанием случайного процесса, а статистические характеристики случайной величины совпадают с характеристиками случайного процесса.

Как правило, в распоряжении исследователя имеется одна реализация случайного процесса конечной длины $x(t)$, которая называется выборочной функцией, или просто выборкой. Если значения выборки берутся в дискретные моменты времени, то мы имеем дело с временным рядом. Вычисляемые по временному ряду (выборке) или по конечному набору временных рядов характеристики CП называются выборочными и служат лишь оценкой истинных характеристик СП.

Классификация случайных процессов приведена на рис. 1.

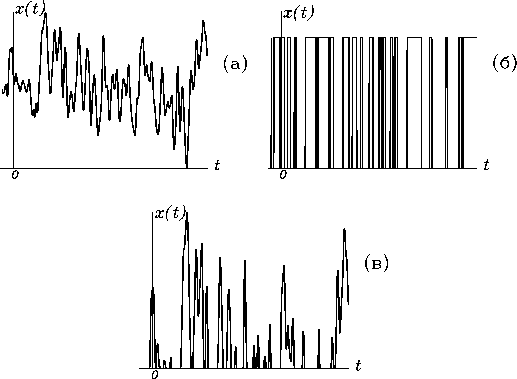
Непрерывнозначный случайный процесс -- это процесс, для которого случайные величины $X(t_i)$ могут принимать любые значения в пределах заданной области возможных значений, например, тепловые шумы в проводниках, дробовые шумы в транзисторах, скорость ветра. Типичная реализация такого СП имеет вид, показанный на рис. 2,  а.

Дискретный случайный процесс -- это процесс, для которого случайные величины могут принимать   только   определенные   значения (возможно их бесконечное число) и никакие другие, например, напряжение, которое случайным образом принимает два значения -- нулевое и ненулевое в зависимости от того, открыт или заперт коммутатор (рис. 2,  б).

Существуют также смешанные случайные процессы, которые имеют как непрерывнозначную, так и дискретную составляющие (рис. 2,  в).

: Рис. 2. Примеры реализаций непрерывнозначного ( а), дискретного ( б) и смешанного ( в) случайных процессов.

Если реализация СП является случайной функцией времени и ее будущие значения могут быть точно предсказаны на основе зарегистрированных раньше значений, то такой СП называется квазидетерминированным. Если предсказание будущих значений невозможно, то процесс называется недетерминированным.

Стационарными называются такие процессы, вероятностные свойства которых не зависят от начала отсчета времени.

Некоторые стационарные СП обладают свойством, заключающимся в том, что каждый член ансамбля реализаций ведет себя в статистическом смысле так же, как и весь ансамбль. В этом случае все характеристики CП можно проанализировать путем исследования свойств только одной реализации. Такие процессы называются эргодическими в строгом смысле^П1. Эргодические в строгом смысле СП всегда являются стационарными. Все нестационарные СП неэргодичны, однако неэргодическими могут быть и стационарные СП.

Пример. Рассмотрим квазидетерминированный СП вида:

$$\begin{eqnarray*} X(t)=Y\cos (\omega t+\Theta ), \end{eqnarray*}$$

$\omega$ -- постоянная, $Y$ -- случайная относительно ансамбля реализаций величина, $\Theta$ -- случайная величина, равномерно распределенная в интервале $[0;2\pi ]$, причем $\Theta$ и $Y$ статистически независимы. Поскольку $Y=Y_k=const$ для отдельной $k$-й реализации, но принимает другие (постоянные) значения для других реализаций, то этот процесс не является эргодическим, однако можно показать, что он является стационарным.

В общем случае трудно доказать, что эргодичность -- обоснованное допущение для какого-либо физического СП, так как на практике обычно возможно измерить лишь одну реализацию этого процесса. Однако часто оказывается полезным предположить эргодичность СП, если только отсутствуют веские доводы физического характера, препятствующие этому. В предположении эргодичности анализ временных рядов значительно упрощается. Мы в этом разделе будем иметь в виду только эргодические и, следовательно, стационарные СП.

Введем в рассмотрение основные статистические характеристики СП -- плотность вероятности, среднее значение, дисперсию, ковариационные и корреляционные функции -- и посмотрим, как их можно вычислять на практике.