П1.2 Плотность вероятности

Значения случайных величин нельзя предугадать даже при полностью известных условиях эксперимента, в котором они измеряются. Возможно указать лишь вероятности того, что случайная величина примет то или иное значение или попадет в заданный интервал. Однако, зная распределение вероятностей случайных величин, возможно делать выводы о свойствах реализаций СП и об их характерных особенностях.

Пусть $X$ -- случайная величина, а $x$ -- любое ее допустимое значение, тогда функция распределения вероятностей $P(x)$ определяет вероятность события, заключающегося в том, что наблюдаемая случайная величина меньше или равна значению $x$, т.е.

$$\begin{eqnarray*} P(x)=Pr (X\le x). \end{eqnarray*}$$

Производная функции $P(x)$ называется одномерной плотностью вероятности (или просто плотностью вероятности) и определяется следующим образом:

$$\begin{eqnarray*} p(x)=\lim_{\Delta x \rightarrow 0} \frac {P(x+\Delta x)-P(x)}{\Delta x}=\frac {dP(x)}{dx}. \end{eqnarray*}$$

Предположим, например, что большое число одинаковых генераторов шума было включено в некоторый момент времени в прошлом и с тех пор они работают до настоящего времени. С выходом всей совокупности генераторов в данный момент времени связывают плотность вероятности $p(x)$, которая характеризует вероятность того, что в определенный момент времени выход $k$-го генератора сигналов $x_k$ лежит в интервале между значениями $a$ и $b$. Плотность вероятности $p(x)$ эргодического процесса $X(t)$ можно также построить, рассматривая относительное время пребывания бесконечной реализации $x(t)$ одного генератора в интервале между значениями $a$ и $b$. В интегральной форме связь вероятности с функцией $p(x)$ записывается следующим образом:

$$\begin{eqnarray*} Pr\{a<x_k \le b\} =\int_{a}^{b} p(x)dx. \end{eqnarray*}$$

Плотность вероятности $p(x)$ задает скорость изменения вероятности в зависимости от значения реализации $x(t)$. Функция $p(x)$ обычно оценивается путем вычисления вероятности того, что мгновенное значение отдельной реализации заключено в узком интервале, центр которого пробегает область значений процесса, с последующим делением на ширину интервала. Общая площадь, ограниченная графиком плотности вероятности, равна единице, что указывает на достоверность события, заключающегося в том, что значения реализации попадают в интервал от $-\infty$ до $\infty$.

Одномерная плотность вероятности, помимо описания вероятностной структуры процесса, обычно применяется с целью проверки нормальности процесса, выявления нелинейностей и анализа экстремальных значений. Однако она не может полностью охарактеризовать свойства СП, поскольку не учитывает статистическую взаимосвязь (корреляцию) между значениями СП в различные моменты времени. Для характеристики степени статистической зависимости вводится понятие совместной плотности вероятности, которая определяет вероятность того, что одновременно выполняются несколько условий. Например, для анализа статистической взаимосвязи между значениями СП, сдвинутыми на интервал времени $\tau$, необходимо рассмотреть двумерную плотность вероятности процессов $X(t)$ и $Y(t)=X(t+\tau)$. Эта функция определяет одновременное выполнение двух условий: случайная величина $X$ принимает значение из интервала $x_1<X\le x_2$ и случайная величина $Y$ лежит в интервале $y_1<Y\le y_2$. В интегральной форме это условие выглядит следующим образом:

$$\begin{eqnarray*}Pr\{x_1<X \le x_2\ , y_1<Y \le y_2\} =\int _{x_1}^{x_2}\int _{y_1}^{y_2} p(x,y,\tau)dxdy. \end{eqnarray*}$$

Аналогично строятся совместные плотности вероятности большей размерности -- многомерные плотности вероятности, характеризующие статистическую взаимосвязь значений СП $\{ X(t+\tau_i)\}$, сдвинутых на различные временные интервалы $\tau_i$, где $i=0,...N$; $N$ определяет размерность плотности вероятности. $N$-мерная плотность вероятности является наиболее полной характеристикой СП, которая учитывает корреляции значений СП в $N$ моментов времени. Чем больше $N$, тем лучше плотность вероятности описывает свойства СП.

Поскольку комбинации временных сдвигов являются произвольными, то можно построить бесконечное число совместных плотностей вероятности различной размерности. Совокупность возможных $N$-мерных плотностей вероятности образует иерархию, которая полностью определяет СП.

: Рис. 3. Примеры реализаций случайных процессов: гармонический сигнал со случайной начальной фазой ( а), белый шум ( б), цветной шум ( в), узкополосный шум ( г), гармонический сигнал со случайной начальной фазой плюс цветной шум ( д), гармонический сигнал со случайной начальной фазой плюс узкополосный шум ( е).

Очевидно, что на основе выборок СП построить иерархию плотностей вероятности невозможно. Однако в некоторых случаях для того, чтобы охарактеризовать процесс, достаточно знать конечное число совместных плотностей вероятности. Это справедливо, например, для СП, состоящих из статистически независимых случайных величин, и для квазидетерминированных СП. Поэтому важно определить принадлежность СП к классу подобных СП.

Среди вероятностных распределений существуют такие, свойства которых очень хорошо изучены и которые наиболее часто используются на практике. К ним относится, прежде всего, нормальное (гауссово) распределение,  распределения Стьюдента  и хи-квадрат, $F$-распределение Фишера, показательное, биномиальное и пуассоновское распределения.

: Рис. 4. Плотности вероятности гармонического сигнала со случайной начальной фазой ( а), белого шума (маркер "o" на рис.  б), цветного шума (сплошная линия на рис.  б), узкополосного шума (пунктирная линия на рис.  б), суммы гармонического сигнала со случайной начальной фазой и цветного шума ( в), суммы гармонического сигнала со случайной начальной фазой и узкополосного шума ( г).

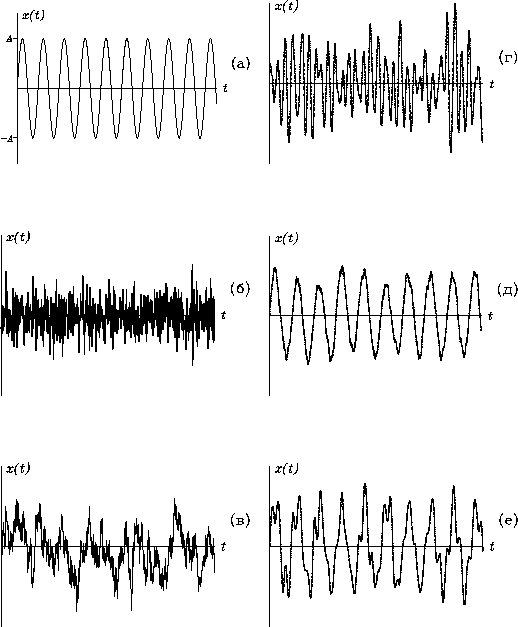
Пример. На рис. 3 показаны типичные реализации некоторых случайных процессов, а также их комбинаций. Основные характерисики этих процессов даны в Приложении.

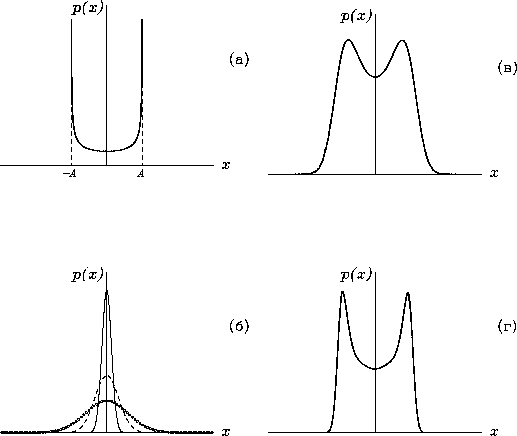
На рис. 4 приведены плотности вероятности случайных процессов, реализации которых представлены на рис. 3.