Вейвлет-преобразование широко используется для анализа нестационарных процессов. Оно показало свою эффективность для решения широкого класса задач, связанных с подавлением шумов, сжатием больших объемов информации, анализом геофизических полей и сигналов, изучением свойств турбулентных полей, обработкой и синтезом сигналов, например речевых, анализом изображений различной природы, например, изображений радужной оболочки глаза, рентгенограмм почки, спутниковых снимков и т. п., а также для решения многих других задач.
Вейвлет-преобразование, как и преобразование Фурье, состоит в вычислении корреляций между анализируемым временным рядом и базисной функцией преобразования. Так, преобразование Фурье направлено на выявление гармонических составляющих временного ряда. Для этой цели применяется бесконечно-осциллирующая гармоническая функция, которая, по-существу, "накладывается" на анализируемую реализацию процесса. Затем проводится сравнение поведения гармонической функции и изучаемой реализации путем вычисления корреляции. Если в результате сравнения выяснено, что они линейно зависимы, т.е. коррелированы между собой, то это означает, что в составе процесса имеются гармонические составляющие выбранной частоты. Затем частота гармонической функции изменяется и процедура сравнения повторяется. Результатом является спектральная функция, которая отражает исходный процесс из временной области в частотную.
Вейвлет-преобразование временного ряда состоит в разложении ряда по базису, сконструированному из обладающей определенными свойствами функции, называемой вейвлетомП1, посредством ее масштабных изменений и переносов. Каждая вейвлет-функция базиса характеризуется определенным масштабом (частотой) и локализацией во времени. В отличие от преобразования Фурье вейвлет-преобразование дает двумерную развертку одномерного процесса, при этом частота и время рассматриваются как независимые переменные. В результате появляется возможность анализировать свойства процесса одновременно во временной и частотной областях.
В основе вейвлет-преобразования лежит идея многомасштабного анализа, которая заключается в последовательном огрублении исходной информации, содержащейся в процессе. Образно говоря, сначала процесс рассматривается под микроскопом, потом -- через лупу, потом -- невооруженным глазом, далее -- с расстояния в несколько шагов. Данный подход позволяет, во-первых, выявлять локальные особенности процесса и классифицировать их по интенсивности, при этом неважно, описывается ли эта особенность степенным рядом или гармонической функцией; во-вторых, отслеживать динамику частотного состава процесса во времени.
Операция огрубления исходной информации осуществляется путем
сглаживания исходного ряда с помощью оконной функции --
вейвлета ![]() . Термином вейвлет обозначают локализованные во временной и
частотной областях солитоноподобные функции, обладающие следующими
свойствами:
. Термином вейвлет обозначают локализованные во временной и
частотной областях солитоноподобные функции, обладающие следующими
свойствами:
-- нулевым средним
![]() ;
;
-- ограниченностью: функция ![]() быстро убывает при
быстро убывает при
![]() ;
;
![]() ;
;
-- автомодельностью: при масштабных преобразованиях вейвлета количество
осцилляций функции ![]() не меняется.
не меняется.
Данные свойства определяют большой класс действительных и комплексных функций, которые являются вейвлетами.
Итак, вейвлет локализован сразу в двух областях --
временной и частотной, и для осуществления вейвлет-преобразования
произвольной реализации процесса ![]() необходимо предусмотреть
возможность сдвигов вейвлет-функций вдоль временной оси и масштабных
преобразований в частотной области путем сжатия или растяжения
исходного вейвлета. Такую возможность реализует базисная
функция следующего вида:
необходимо предусмотреть
возможность сдвигов вейвлет-функций вдоль временной оси и масштабных
преобразований в частотной области путем сжатия или растяжения
исходного вейвлета. Такую возможность реализует базисная
функция следующего вида:
в которой параметры ![]() и
и ![]() являются действительными
числами и определяют масштаб (величину, обратно пропорциональную
частоте) и временной сдвиг, соответственно. На основе этой базисной
функции вейвлет-преобразование непрерывной функции
являются действительными
числами и определяют масштаб (величину, обратно пропорциональную
частоте) и временной сдвиг, соответственно. На основе этой базисной
функции вейвлет-преобразование непрерывной функции ![]() ,
определенной на всей временной оси
,
определенной на всей временной оси
![]() , записывается в
виде:
, записывается в
виде:
здесь
![]() -- коэффициенты вейвлет-преобразования; символом "*"
отмечена комплексно-сопряженная функция. Параметр
-- коэффициенты вейвлет-преобразования; символом "*"
отмечена комплексно-сопряженная функция. Параметр ![]() меняется в
интервале
меняется в
интервале
![]() , пробегая всю временную ось, т.е. всю
временную область, на которой определена функция
, пробегая всю временную ось, т.е. всю
временную область, на которой определена функция ![]() . Параметр
. Параметр ![]() меняется от
меняется от ![]() до
до ![]() , но обычно рассматривается только
положительная область. Индекс
, но обычно рассматривается только
положительная область. Индекс ![]() у коэффициентов
у коэффициентов ![]() подчеркивает, что значение
подчеркивает, что значение
![]() зависит от выбора функции
зависит от выбора функции ![]() .
При использовании действительного вейвлета получается двумерный массив
коэффициентов
.
При использовании действительного вейвлета получается двумерный массив
коэффициентов ![]() , а при применении комплексного --
двумерные массивы значений модуля
, а при применении комплексного --
двумерные массивы значений модуля ![]() и фазы
и фазы ![]() :
:
Процедура вычисления коэффициентов вейвлет-преобразования по формуле
(2.26) для каждой пары параметров ![]() и
и ![]() выглядит
следующим образом:
выглядит
следующим образом:
-- растянуть вейвлет ![]() в
в ![]() раз по горизонтали и в
раз по горизонтали и в ![]() раз по
вертикали;
раз по
вертикали;
-- сдвинуть вейвлет в точку ![]() ; получаем вейвлет
; получаем вейвлет ![]() ;
;
-- усреднить значение функции ![]() c помощью временного окна
c помощью временного окна
![]() .
.
Далее процедура повторяется для другой пары параметров ![]() и
и
![]() .
.
Обратное вейвлет-преобразование записывается с помощью той же базисной
функции, что и прямое:
| (П29) |
Коэффициенты вейвлет-преобразования временного ряда ![]() длины
длины ![]() вычисляются по формуле (шаг дискретизации равен единице):
вычисляются по формуле (шаг дискретизации равен единице):
в которой параметр сдвига ![]() принимает целые значения из
области
принимает целые значения из
области ![]() , а параметр масштаба
, а параметр масштаба ![]() -- любое значение из
области
-- любое значение из
области ![]() .
.
Коэффициенты вейвлет-преобразования содержат информацию об
анализируемом процессе и используемом вейвлете. Поэтому выбор
анализирующего вейвлета определяется тем, какую информацию необходимо
извлечь из процесса. Каждый вейвлет имеет характерные особенности во
временной и частотной областях, поэтому иногда с помощью разных
вейвлетов можно полнее выявить и подчеркнуть те или иные свойства
анализируемого процесса. Если провести аналогию с микроскопом, а
вейвлет часто называют математическим микроскопом, то параметр
сдвига ![]() фиксирует точку наведения микроскопа, параметр масштаба
фиксирует точку наведения микроскопа, параметр масштаба ![]() -- его увеличение и, наконец, базисный вейвлет
-- его увеличение и, наконец, базисный вейвлет ![]() определяет
оптические свойства микроскопа.
определяет
оптические свойства микроскопа.
Рассмотрим несколько примеров вейвлетообразующих функций. Простейшим
является HAAR-вейвлет, названный так по имени
предложившего его Хаара, и
определяемый соотношением:
Этот вейвлет имеет резкие границы во
временной области и, как следствие, бесконечно осциллирующие, но
убывающие хвосты в частотной области. Кроме того, HAAR-вейвлет является
несимметричным. Часто применяется очень похожий, но симметричный
FHAT-вейвлет (French HAT -- французская шляпа):
Фурье-образ ![]() этого вейвлета имеет вид:
этого вейвлета имеет вид:
здесь ![]() -- функция Хевисайда. Если правые
чпсти формул (2.32) и (2.33) поменять местами, то
получим вейвлет Литтвуда-Пели (LP-вейвлет), который в противоположность
FHAT-вейвлету имеет резкие границы в частотной области и медленно
спадает во временной области. FHAT- и LP-вейвлеты можно считать
предельными случаями, между которыми находятся практически все
вейвлет-функции.
-- функция Хевисайда. Если правые
чпсти формул (2.32) и (2.33) поменять местами, то
получим вейвлет Литтвуда-Пели (LP-вейвлет), который в противоположность
FHAT-вейвлету имеет резкие границы в частотной области и медленно
спадает во временной области. FHAT- и LP-вейвлеты можно считать
предельными случаями, между которыми находятся практически все
вейвлет-функции.
Наиболее часто среди вещественных вейвлетов используются вейвлеты,
сконструированные на основе производных функций Гаусса:
здесь
![]() .
Более высокие производные позволяют
извлечь информацию об особенностях высокого порядка, содержащихся во
временном ряде. Вейвлеты на основе функций Гаусса используются для
анализа масштабных свойств временных рядов, в том числе
мультифрактальных: типа особенности (степенная, импульсная, ступенька
и т. п.), ее интенсивности, распределения особенностей по масштабам и
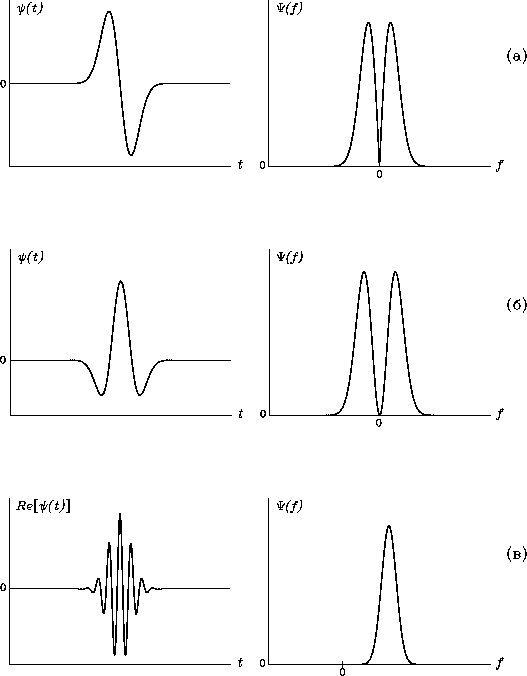
т. д. На рис. 19, а и рис. 19, б показаны вейвлеты и их
фурье-образы, полученные для
.
Более высокие производные позволяют
извлечь информацию об особенностях высокого порядка, содержащихся во
временном ряде. Вейвлеты на основе функций Гаусса используются для
анализа масштабных свойств временных рядов, в том числе
мультифрактальных: типа особенности (степенная, импульсная, ступенька
и т. п.), ее интенсивности, распределения особенностей по масштабам и
т. д. На рис. 19, а и рис. 19, б показаны вейвлеты и их
фурье-образы, полученные для ![]() и
и ![]() . По внешнему виду первый из
них называют обычно WAVE-вейвлетом (WAVE-волна), второй --
мексиканской шляпой, или MHAT-вейвлетом (Mexican HAT).
. По внешнему виду первый из
них называют обычно WAVE-вейвлетом (WAVE-волна), второй --
мексиканской шляпой, или MHAT-вейвлетом (Mexican HAT).
Среди комплексных вейвлетов наибольшее распространение получил вейвлет
Морле:
 |
Результаты вейвлет-преобразований во многом
зависят от используемого вейвлета, однако
вейвлет-преобразования обладают некоторыми универсальными свойствами,
которые не зависят от вида вейвлета. Рассмотрим некоторые из
этих свойств. Будем использовать обозначение
![]() .
.
1. Линейность:
| (П36) |
2. Инвариантность относительно сдвига:
| (П37) |
Из этого свойства следует коммутативность дифференцирования,
в частности,
![]() . Поскольку
коэффициенты вейвлет-преобразования являются гладкими
функциями параметров даже для негладкой функции
. Поскольку
коэффициенты вейвлет-преобразования являются гладкими
функциями параметров даже для негладкой функции ![]() , то это свойство
можно использовать для численного дифференцирования негладких функций с
разрывами производной.
, то это свойство
можно использовать для численного дифференцирования негладких функций с
разрывами производной.
3. Инвариантность относительно растяжения (сжатия):
![$\displaystyle W\left[x\left(\frac{t}{a_0} \right)\right]=\frac{1}{a_0}W\left(
\frac{a}{a_0},\frac{b}{a_0} \right).$](img673.gif) |
(П38) |
Это свойство позволяет выявлять
особенности ряда и их характер путем анализа поведения
коэффициентов вейвлет-преобразования
при
![]() вместо анализа функции
вместо анализа функции ![]() .
.
4. Частотно-временная локализация и наличие частотно-временного окна. Как известно, чем лучше функция сконцентрирована во времени, тем больше она "размазана" в частотной области. При переходе от одного масштаба к другому произведение временного и частотного разрешения (площадь частотно-временного окна) остается постоянным. Данное ограничение учитывается вейвлетным базисом, который извлекает высокочастотную информацию из относительно малых временных интервалов и наоборот, низкочастотную спектральную информацию из относительно широких интервалов. В результате вейвлет-преобразование позволяет проследить изменение частотного состава временного ряда с течением времени.
5. Дифференцирование:
Это свойство означает, что вместо дифференцирования исходного временного ряда, например, для удаления полиномиального тренда, можно продифференцировать нужное число раз вейвлет.
6. Энергетическое свойство:
из которого следует, что энергия процесса на каком-либо
масштабе может быть рассчитана через коэффициенты
вейвлет-преобразования;
![]() можно интерпретировать
как плотность энергии процесса в частотно-временном пространстве.
Если провести усреднение вейвлет-коэффициентов по времени,
то получим распределение энергии по масштабам или так называемый
глобальный вейвлет-спектр:
можно интерпретировать
как плотность энергии процесса в частотно-временном пространстве.
Если провести усреднение вейвлет-коэффициентов по времени,
то получим распределение энергии по масштабам или так называемый
глобальный вейвлет-спектр:
Глобальный вейвлет-спектр соответствует спектру мощности, сглаженному на каждой частоте с помощью оконной функции, которая определяется фурье-образом вейвлета. Поэтому спектры, вычисленные с помощью вейвлет-преобразования, являются гораздо более гладкими, чем спектры, полученные через преобразование Фурье.
=.45
 =.45
=.45
 =.5
=.5
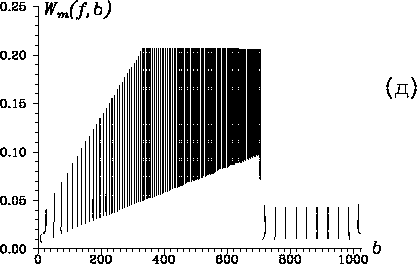

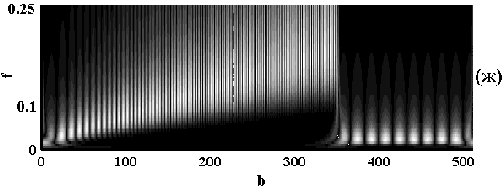
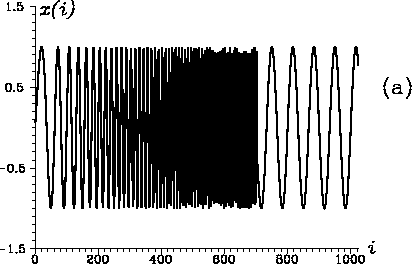
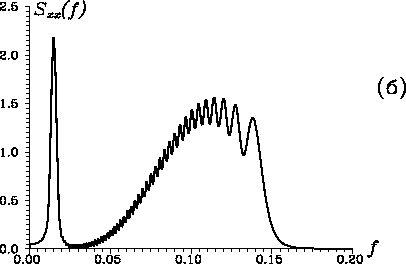
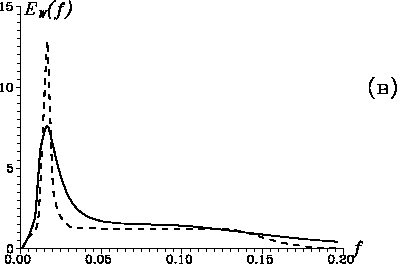
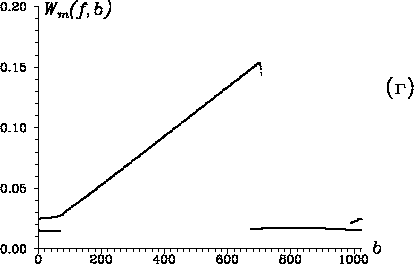
Рис. 20. Временной ряд ![]() с
меняющейся во времени частотой ( а), его спектр мощности,
рассчитанный с помощью преобразование Фурье ( б),
глобальные вейвлет-спектры ( в), рассчитанные с
помощью MHAT-вейвлета (сплошная линия) и вейвлета Морле (пунктирная
линия), скелетоны коэффициентов вейвлет-преобразования, рассчитанные с
помощью вейвлета Морле ( г) и MHAT-вейвлета ( д),
частотно-временные вейвлет-спектры, полученные с помощью
вейвлета Морле ( е) и MHAT-вейвлета ( ж). Более светлый
цвет на рисунках ( е) и ( ж) соответствует
б
с
меняющейся во времени частотой ( а), его спектр мощности,
рассчитанный с помощью преобразование Фурье ( б),
глобальные вейвлет-спектры ( в), рассчитанные с
помощью MHAT-вейвлета (сплошная линия) и вейвлета Морле (пунктирная
линия), скелетоны коэффициентов вейвлет-преобразования, рассчитанные с
помощью вейвлета Морле ( г) и MHAT-вейвлета ( д),
частотно-временные вейвлет-спектры, полученные с помощью
вейвлета Морле ( е) и MHAT-вейвлета ( ж). Более светлый
цвет на рисунках ( е) и ( ж) соответствует
б
![]() льшим
значениям коэффициентов вейвлет-преобразования.
льшим
значениям коэффициентов вейвлет-преобразования.
Способы графического представления
результатов вейвлет-преобразования могут быть самыми различными.
Вейвлет-спектр ![]() представляет собой поверхность в трехмерном пространстве. Вместо
изображения поверхности часто используется, во-первых, проекция на
плоскость с изображением изоуровней, которые позволяют
проследить изменения интенсивностей коэффициентов вейвлет-преобразования
на разных временных масштабах, и, во-вторых,
картины локальных экстремумов поверхностей, так называемый
скелетон, четко выделяющий структуру анализируемого процесса.
представляет собой поверхность в трехмерном пространстве. Вместо
изображения поверхности часто используется, во-первых, проекция на
плоскость с изображением изоуровней, которые позволяют
проследить изменения интенсивностей коэффициентов вейвлет-преобразования
на разных временных масштабах, и, во-вторых,
картины локальных экстремумов поверхностей, так называемый
скелетон, четко выделяющий структуру анализируемого процесса.
Рассмотрим возможности вейвлет-преобразования в выявлении
характерных особенностей процессов. В качестве реализации СП
рассмотрим нестационарный временной ряд
![]() ,
частота
,
частота ![]() которого сначала линейно растет, а потом
скачком выходит на постоянное значение. На рис. 20 представлен ряд
которого сначала линейно растет, а потом
скачком выходит на постоянное значение. На рис. 20 представлен ряд
![]() , его спектр мощности
, его спектр мощности ![]() П1, рассчитанный через преобразование Фурье,
глобальные вейвлет-спектры
П1, рассчитанный через преобразование Фурье,
глобальные вейвлет-спектры ![]() и скелетоны
и скелетоны ![]() ,
полученные с помощью MHAT-вейвлета и вейвлета Морле, а также
частотно-временные спектры
,
полученные с помощью MHAT-вейвлета и вейвлета Морле, а также
частотно-временные спектры ![]() . Видно (рис. 20, а), что
спектр мощности, вычисленный через преобразование Фурье, дает неверную
информацию о частотном составе реализации: энергия высокочастотных
компонент значительно превышает истинную. Глобальные вейвлет-спектры
(рис. 20, б) показывают правильное соотношение между
энергиями низко- и высокочастотных составляющих ряда. Скелетон
(рис. 20, г) и коэффициенты вейвлет-преобразования (рис. 20,
е), рассчитанные с помощью вейвлета Морле, дают локализацию
гармонических составляющих ряда во времени. Изображения коэффициентов
. Видно (рис. 20, а), что
спектр мощности, вычисленный через преобразование Фурье, дает неверную
информацию о частотном составе реализации: энергия высокочастотных
компонент значительно превышает истинную. Глобальные вейвлет-спектры
(рис. 20, б) показывают правильное соотношение между
энергиями низко- и высокочастотных составляющих ряда. Скелетон
(рис. 20, г) и коэффициенты вейвлет-преобразования (рис. 20,
е), рассчитанные с помощью вейвлета Морле, дают локализацию
гармонических составляющих ряда во времени. Изображения коэффициентов
![]() и их скелетона, полученные с помощью MHAT-вейвлета
(рис. 20, д, ж), более непривычные, но отражают ту же
информацию. MHAT-вейвлет позволяет также оценить характер
"скачка" частоты, реагируя на изменение формы реализации, а не ее
частотного состава.
и их скелетона, полученные с помощью MHAT-вейвлета
(рис. 20, д, ж), более непривычные, но отражают ту же
информацию. MHAT-вейвлет позволяет также оценить характер
"скачка" частоты, реагируя на изменение формы реализации, а не ее
частотного состава.