П2.7 Функция спектральной плотности

Функция спектральной плотности иначе называется спектром мощности; наряду с плотностью вероятности, корреляционными функциями, математическим ожиданием и дисперсией, спектр мощности относится к характеристикам, с помощью которых анализируются основные свойства стационарных случайных процессов. Спектральная плотность применяется для анализа систем, подвергнутых действию случайных сигналов, для определения свойств систем по входным и выходным процессам, идентификации источников энергии и шума; знание спектральной плотности помехового сигнала позволяет определить физическую природу этого сигнала и осуществить его подавление или фильтрацию; спектр мощности используется для оценки соотношения между периодическими и шумовыми составляющими случайного процесса.

Подобно спектральной функции, которая определяется преобразованием Фурье, функция спектральной плотности характеризует гармонический состав исследуемого процесса. Различие этих функций состоит в том, что преобразование Фурье определяет амплитудный спектр, а спектральная плотность -- энергетический спектр. В отличие от преобразования Фурье спектральная плотность характеризует спектральный состав всего СП, т.е. ансамбля реализаций, а не какой-то одной реализации СП. Кроме того, нахождение частотного состава процесса через спектральную плотность является более физичным, поскольку измерительные аналоговые приборы работают на основе определения величины энергии процесса, а не амплитуды.

Функции спектральной плотности можно вводить в рассмотрение тремя различными способами: c помощью ковариационных функций, через преобразование Фурье и с помощью фильтрации.

1. Определение спектров через ковариационные функции

Этот способ определения спектральной плотности составляет операция взятия преобразования Фурье от предварительно вычисленной ковариационной функции. Пусть известны ковариационные функции $R_{xx}(\tau)$ и $R_{yy}(\tau)$ случайных процессов $X(t)$ и $Y(t)$, соответственно, а также их взаимные ковариационные функции $R_{xy}(\tau)$ и $R_{yx}(\tau)$. Преобразования Фурье функций $R(\tau)$ в соответствии с (1.33) определяются формулами:

$$S_{xx}(f)=\int _{-\infty }^{\infty }R_{xx}(\tau)e^{-j2\pi f\tau}d\tau,$$

$$S_{yy}(f)=\int _{-\infty }^{\infty }R_{yy}(\tau)e^{-j2\pi f\tau}d\tau,$$

$$S_{xy}(f)=\int _{-\infty }^{\infty }R_{xy}(\tau)e^{-j2\pi f\tau}d\tau,$$

$$S_{yx}(f)=\int _{-\infty }^{\infty }R_{yx}(\tau)e^{-j2\pi f\tau}d\tau.$$ (П56)

Функции $S_{xx}(f)$ и $S_{yy}(f)$ называются двусторонними спектральными плотностями случайных процессов $X(t)$ и $Y(t)$, соответственно, т. к. они определены как для положительных, так и для отрицательных частот. Функции $S_{xy}(f)$ и $S_{yx}(f)$ называются двусторонними взаимными спектральными плотностями случайных процессов $X(t)$ и $Y(t)$.

Обратные преобразования Фурье имеют вид:

$$R_{xx}(\tau)=\int _{-\infty }^{\infty }S_{xx}(f)e^{j2\pi f\tau}df,$$

$$R_{yy}(\tau)=\int _{-\infty }^{\infty }S_{yy}(f)e^{j2\pi f\tau}df,$$

$$R_{xy}(\tau)=\int _{-\infty }^{\infty }S_{xy}(f)e^{j2\pi f\tau}df,$$

$$R_{yx}(\tau)=\int _{-\infty }^{\infty }S_{yx}(f)e^{j2\pi f\tau}df.$$ (П57)

Соотношения (1.56) и (1.57), называемые формулами Винера - Хинчина, имеют фундаментальное значение для анализа случайных сигналов, т. к. они устанавливают связь между представлением случайного процесса во временной области (с помощью ковариационных функций) и в частотной области (с помощью спектральных плотностей). Из формул Винера - Хинчина (1.57) становится ясным физический смысл спектральной плотности:

$$R_{xx}(0)=\int _{-\infty }^{\infty }S_{xx}(f) df.$$ (П58)

Интеграл по всем частотам в правой части выражения (1.58) равен ковариационной функции при $\tau =0$, т.е. cредней энергии процесса. Таким образом, функция спектральной плотности (спектр мощности) характеризует распределение средней энергии случайного процесса по частотам. Термин мощность в названии "спектр мощности" используется условно; своим происхождением он обязан электротехнике. Дело в том, что рассеяние мощности на элементе электрической цепи пропорционально среднему квадрату напряжения, т.е. средней энергии, и происходит подмена термина "средняя энергия" на термин "мощность". Слово спектр подчеркивает, что функция $S_{xx}(f)$ является функцией частот.

: Рис. 14. Функции спектральной плотности гармонического сигнала со случайной начальной фазой ( а), белого шума ( б), цветного шума ( в), узкополосного шума ( г), суммы гармонического сигнала со случайной начальной фазой и цветного шума ( д), суммы  гармонического  сигнала  со случайной начальной фазой и узкополосного шума ( е).

Отметим, что в случае нестационарного процесса корреляционные функции не могут быть  восстановлены  по известной  спектральной плотности.

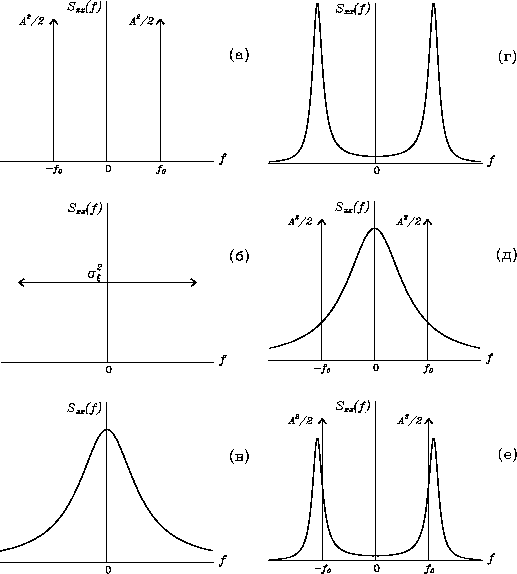
На рис. 14 показаны функции спектральной плотности для некоторых случайных процессов. Например, спектр мощности гармонического процесса (.1) представляет собой сумму двух дельта-функций, расположенных на частотах $\pm f_0$ (см. формулу (.4)).

Точно  такую  же  спектральную  плотность   имеет  функция $x(t)=A\sin (\omega t +\varphi_0)$. Это означает, что в отличие от преобразования Фурье (1.33) спектр мощности не содержит информацию о фазовых составляющих случайного процесса. Кроме того, если модуль спектральной функции $X(f)$ определяет спектр амплитуд, то спектральная плотность определяет спектр средних энергий гармонических составляющих. Множители перед дельта-функциями в формулах (1.41), (1.42) и (.4) указывают на то, что в отличие от преобразования Фурье $X(f)$, которое в общем случае является комплексным, спектральная плотность $S_{xx}(f)$ -- всегда вещественная четная функция.

В отличие от спектральной плотности $S_{xx}(f)$, взаимные спектральные плотности не обязательно должны быть вещественными положительными и четными функциями частоты $f$. Они обладают следующими свойствами.

1. $S_{xy}(f)=S^*_{yx}(f)$; здесь знак "*" указывает на комплексно-сопряженную величину. Это свойство показывает, что вместо вычисления двух функций $S_{xy}(f)$ и $S_{yx}(f)$ достаточно вычислить лишь одну из них, а вторую можно определить через вычисленную.

2. Вещественные части $Re[S_{xy}(f)]$ и $Re[S_{yx}(f)]$ являются четными функциями частоты $f$.

3. Мнимые части  $Im[S_{xy}(f)]$ и  $Im[S_{yx}(f)]$ являются нечетными функциями частоты $f$.

4. Для всех частот выполняется неравенство

$$\vert S_{xy}(f)\vert^2\le S_{xx}(f)S_{yy}(f),$$

что позволяет перейти к нормированной взаимной функции -- функции когерентности, которая меняется в пределах от $0$ до $1$ (см. ниже).

Взаимную спектральную плотность можно представить в комплексной форме:

$$\begin{eqnarray*} S_{xy}(f)=\vert S_{xy}(f)\vert\exp(-j\Theta_{xy}(f)), \end{eqnarray*}$$

в которой модуль и фазовый угол определяются соотношениями:

$$\vert S_{xy}(f)\vert = \sqrt{ (Re [S_{xy}(f)])^2+(Im [S_{xy}(f)])^2)},$$ (П59)

$$\Theta_{xy}(f) = {\rm arctg} \frac{Im [S_{xy}(f)]}{Re [S_{xy}(f)]}.$$ (П60)

Формулы (1.59) и (1.60) определяют взаимный спектр амплитуд и фаз, соответственно. Спектр амплитуд характеризует энергетическое взаимодействие гармонических компонент двух процессов, а спектр фаз -- временной сдвиг между компонентами.

На практике, как правило, вместо двусторонней спектральной плотности $S_{xx}(f)$  используют   одностороннюю спектральную плотность $G_{xx}(f)$, которая определена только для положительных частот:

$$\begin{eqnarray*} G_{xx}(f)=\left\{ \begin{array}{cc} 2 S_{xx}(f), & f\ge 0.\\ 0,& f<0. \end{array}\right. \end{eqnarray*}$$

Аналогичным образом вводится односторонняя взаимная спектральная плотность $G_{xy}(f)$.

2. Определение спектров через финитное преобразование Фурье

Определение спектральной плотности через ковариационные функции является более понятным по сравнению с подходом, который мы сейчас рассмотрим. Данный подход, основанный на определении спектральной функции через преобразование Фурье ряда конечной длины, т.е. через финитное преобразование Фурье, дает ясную физическую интерпретацию спектра мощности.

Посмотрим, как можно получить представление случайного процесса $X(t)$ в частотной области. Напомним, что под случайным процессом понимается ансамбль реализаций. На первый взгляд кажется естественным для частотного представления использовать прямое преобразование Фурье (1.33) выбранной реализации $x(t)$ случайного процесса. Однако задача состоит в нахождении спектральной характеристики, которая должна отражать свойства процесса в целом, а не какой-либо его отдельной реализации, поскольку целью анализа временных рядов является определение характеристик процесса, которому принадлежит рассматриваемый временной ряд. Задача нахождения характеристик временного ряда без соотнесения его с каким-либо, пусть гипотетическим, процессом лишена физического смысла. Преобразование Фурье (1.33) дает разные результаты для каждой из реализаций СП, поэтому его можно использовать только как частотное представление отдельной реализации, но не всего случайного процесса. Это означает, что для получения статистической характеристики СП к процедуре преобразования Фурье отдельной реализации необходимо каким-то образом добавить процедуру усреднения по ансамблю. Кроме того, для стационарных случайных процессов преобразование Фурье (1.33) не существует, поскольку не выполняется условие абсолютной интегрируемости (1.35). Это условие не удовлетворяется для любой не равной нулю реализации СП. На практике невыполнение этого условия означает, что полученная характеристика является несостоятельной: разброс (дисперсия) функции сравним со средним значением функции, т.е. ошибка оценки велика.

Для того, чтобы преобразование существовало для каждой реализации, необходимо их видоизменить. Рассмотрим новый случайный процесс $X_T(t)$, реализации которого ограничены на временном интервале $\vert t\vert\le T<\infty$:

$$\begin{eqnarray*} X_T(t)=\left\{ \begin{array}{cc} X(t), &\vert t\vert\le T, \\ 0, &\vert t\vert>T. \end{array}\right. \end{eqnarray*}$$

Для усеченного  процесса $X_T(t)$  будет   существовать преобразование Фурье $F_X(f)$, поскольку выполняется условие интегрируемости в среднеквадратическом:

$$\int_{-\infty}^{\infty} \vert X_T(t)\vert^2 dt<\infty,$$ (П61)

которое является более строгим, чем условие абсолютной интегрируемости (1.35). Далее необходимо перейти к пределу $T\rightarrow \infty$ для того, чтобы построенные в пределе функции являлись оценками исходного случайного процесса.

Оказывается, что такой предельный переход возможен, если вместо функции $F_X(f)$ рассматривать другую функцию:

$$\vert F_X(f)\vert^2=F_X(f)F_X(-f),$$

которая связана с процессом $X_T(t)$ через равенство Парсеваля:

$$\int_{-T}^{T}X^2_T(t)dt =\int_{-\infty}^{\infty} \vert F_X(f)\vert^2 df.$$ (П62)

Если выражение (1.62) разделить на $2T$, то его левая часть будет характеризовать среднюю энергию процесса на временном интервале от $-T$ до $T$. Для эргодического процесса эта величина приближается к значению среднего квадрата СП $\langle x^2(t)\rangle$ при $T\rightarrow \infty$ [1,8]. Но переход к пределу $T\rightarrow \infty$ непосредственно в выражении (1.62) невозможен, поскольку преобразование Фурье $F_X(f)$ не существует в этом пределе. Кроме того, необходимо помнить, что $F_X(f)$ является случайной функцией относительно ансамбля реализаций и, следовательно, содержит ошибку. Поэтому необходимо провести процедуру усреднения по ансамблю реализаций. Строго математически можно показать [8], что переход к пределу $T\rightarrow \infty$ возможен, если рассмотреть предел математического ожидания величины $(1/T)\vert F_X^2(f)\vert$, поскольку существует интеграл от $\vert F_X^2(f)\vert$, как следует из условия (1.61). Учитывая это, разделим обе части соотношения (1.62) на $2T$, усредним выражение (1.62) по ансамблю путем вычисления математического ожидания и, переходя к пределу при $T\rightarrow \infty$, получим соотношение:

$$E[ \langle x^2\rangle ]=\int_{-\infty}^{\infty} \lim_{T\rightarrow \infty} \frac{E[\vert F_X(f)\vert^2]}{2T} df.$$ (П63)

Левая часть выражения (1.63) записана с учетом формулы (1.17), в которой $\tau =0$.

Для стационарного СП математическое ожидание среднего квадрата реализации равно самому среднему квадрату $E[ \langle x^2\rangle ] = \langle x^2\rangle$, т.е. средней энергии СП. Сравним полученное выражение (1.63) c (1.58). Левые части этих соотношений являются средней энергией СП. Поэтому их правые части имеют один и тот же физический смысл и характеризуют распределение средней энергии СП по частотам. Таким образом, подынтегральное выражение в правой части (1.63) является искомым представлением случайного процесса в частотной области -- функцией спектральной плотности (спектром мощности) $S_{xx}(f)$ процесса $X(t)$:

$$S_{xx}(f)= \lim_{T\rightarrow \infty} \frac{E[\vert F_X(f)\vert^2]}{2T}.$$ (П64)

Как видно, спектр мощности является усредненным по времени математическим ожиданием от квадрата преобразования Фурье усеченной реализации. Отметим, что переход к пределу при $T\rightarrow \infty$ возможен только после операции усреднения по ансамблю. Это означает, что при практических расчетах спектра мощности случайного процесса через преобразование Фурье реализаций этого процесса необходимо предусмотреть процедуру усреднения по ансамблю.

Таким образом, спектральный состав СП не может быть представлен через амплитудный спектр, который получается в результате преобразования Фурье отдельной реализации СП; необходимо использовать более сложную процедуру определения спектрального состава через вычисление спектра мощности. С радиофизической точки зрения это означает, что спектральная характеристика СП представляет собой плотность энергии, а не плотность напряжения.

Взаимные спектральные плотности двух случайных процессов $X(t)$ и $Y(t)$ выражаются через преобразование Фурье усеченных реализаций следующим образом:

$$S_{xy}(f)= \lim_{T\rightarrow \infty} \frac{E[F_X(-f)F_Y(f)]}{2T},$$

$$S_{yx}(f)= \lim_{T\rightarrow \infty} \frac{E[F_Y(-f)F_X(f)]}{2T}.$$

3. Определение спектров с помощью фильтрации

Поскольку спектральная плотность  характеризует  распределение средней энергии по частотам, ее можно определить через процедуру узкополосной фильтрации и усреднение энергии отфильтрованного сигнала. Обычно такая процедура реализуется в аналоговых устройствах и включает следующие операции:

-- получение реализации $x(t)$ длительности $T$;

-- выбор полосно-пропускающего линейного фильтра с центральной частотой $f_0$ и полосой пропускания $\Delta f$. Чем уже полоса $\Delta f$ используемого фильтра, тем выше частотное разрешение спектра мощности;

-- частотную фильтрацию реализации $x(t)$ с помощью полосно-пропускающего фильтра с граничными частотами $(f_0-\Delta f)$ и $(f_0+\Delta f)$. В результате этой операции получается отфильтрованная реализация $x(f_0,\Delta f,t)$;

-- возведение в квадрат мгновенного значения отфильтрованной реализации. В результате получается реализация $x^2(f_0,\Delta f,t)$;

-- усреднение реализации $x^2(f_0,\Delta f,t)$ по ее длительности $T$. В результате получается оценка средней энергии отфильтрованной реализации;

-- деление величины средней энергии на ширину полосы пропускания фильтра $\Delta f$, в результате чего получается оценка плотности средней энергии в частотном диапазоне от $(f_0-\Delta f)$ до $(f_0+\Delta f)$, т.е. оценка спектра мощности на частоте $f_0$:

$$\begin{eqnarray*} \hat{S}_{xx}(f_0)= \frac{1}{\Delta f T}\int_{0}^{T}x^2 (f_0,\Delta f,t) dt. \end{eqnarray*}$$

Далее описанная процедура повторяется для других значений центральных частот фильтра $f_i=\pm\Delta f(1+2i)$:

$$\hat{S}_{xx}(f_i)= \frac{1}{\Delta f T}\int_{0}^{T}x^2 (f_i,\Delta f,t) dt;$$ (П65)

здесь $i=1,2,...,M$. Значение $M$ определяет максимальную частоту спектра мощности. В случае дискретной реализации значение $M$ определяется частотой Найквиста.

Отметим, что оценку двустороннего спектра мощности (1.65) можно получить только при цифровой обработке реализации с использованием фильтров с отрицательной центральной частотой. Если применяется аналоговая обработка реализации, то получается оценка односторонего спектра мощности.

Для вычисления взаимной спектральной плотности нужно обобщить описанную процедуру на случай двух сигналов:

$$\hat{S}_{xy}(f) = Re[\hat{S}_{xy}(f)]-j Im[\hat{S}_{xy}(f)],$$

$$Re[\hat{S}_{xy}(f)] = \frac{1}{\Delta f T}\int_{0}^{T}x (f_0,\Delta f,t)y (f_0,\Delta f,t) dt,$$

$$Im [\hat{S}_{xy}(f)] = \frac{1}{\Delta f T}\int_{0}^{T}x (f_0,\Delta f,t)y^0 (f_0,\Delta f,t) dt,$$

где $y^0(f_0,\Delta f,t)$ -- сдвинутый по фазе на $90^{\rm o}$ отфильтрованный сигнал $y(f_0,\Delta f,t)$.