П2.6 Эффект утечки. Оконные функции

Мы уже рассмотрели эффекты, которые возникают при анализе непрерывных реализаций конечной длины. Для дискретных процессов эти явления проявляются еще в большей степени и могут приводить к ошибочным трактовкам результатов анализа. В дискретной области эффекты, связанные с конечной длиной реализации, называются эффектами утечки. В случае периодического дискретного процесса этих эффектов удается избежать при специальном выборе шага дискретизации и длины временного ряда. Действительно, рассмотрим спектральную функцию временного ряда, состоящего из значений гармонической функции $x(i)=A\cos (2\pi i f_0)$ c частотой $f_0=m/(NT)$; здесь $N$ -- длина ряда и $T$ -- период дискретизации. В этом случае временной ряд длительности $P=NT$ содержит целое число $m$ периодов косинусоиды: $m=Pf_0 =NTm/(NT)$, а выражение (1.48) для дискретной спектральной функции имеет вид:

$$X_P(f_k)= \frac{A}{2}\left[ \frac {\sin (\pi(f_k-f_0)P)}{\pi (f_k-f_0)}+\frac {\sin (\pi(f_k+f_0)P)}{\pi (f_k+f_0)} \right],~~ f_k=\frac{k}{NT}.$$ (П51)

Выразим значения частот $f_k$, $f_0$ и длительность временного ряда $P$ через $N$ и $T$. Тогда выражение (1.51) преобразуется к виду:

$$X_P(f_k)=\left\{ \begin{array}{cc} A P/2, & k=\pm m,\\ 0, &k\neq \pm m. \end{array}\right.$$ (П52)

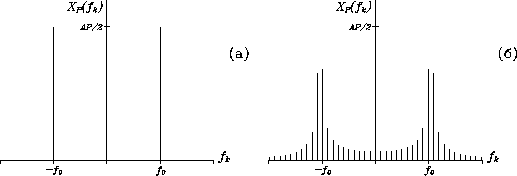
Соотношение (1.52) показывает, что спектральная функция определена только на частоте косинусоиды и эффект размывания спектра отсутствует (рис. 11,  а).

Теперь рассмотрим тот же временной ряд, увеличив его длительность на половину периода гармонической функции. Спектр такого временного ряда, вычисленный по формуле (1.51), показан на рис. 11,  б. Как видно, появились новые спектральные составляющие (боковые лепестки), а высота пиков на частотах $\pm f_0$ уменьшилась. В этом случае можно говорить о вытекании энергии из спектрального пика косинусоиды. Если бы имелась еще одна косинусоида, но с другой частотой, то энергия, которая вытекла из частот $\pm f_0$, добавилась бы к энергии второй косинусоиды. В этом случае говорят о втекании энергии. Вытекание и втекание энергии спектральных составляющих является эффектом утечки. Этот эффект проявляется, если анализируемый временной ряд не содержит целых циклов периодических компонент, образующих временной ряд, или шаг дискретизации не связан с периодом этих компонент соотношением $f_0=m/(NT)$. Очевидно, что эффекта утечки невозможно избежать для квазипериодических и непериодических временных рядов.

: Рис. 11. Преобразование Фурье ряда, состоящего из дискретных значений функции косинус, для двух случаев: ряд имеет длительность, кратную целому числу периодов косинусоиды ( а); длительность ряда не кратна целому числу периодов косинусоиды ( б).

Явление утечки обусловлено наличием разрывов на концах временного ряда, являющихся следствием конечной длины записи. Ограничение длины ряда во временной области, как было показано, достигается при помощи прямоугольного окна, что ведет к появлению колебаний вида $(\sin x)/x$ в спектральной области. Эти колебания определяют конечную ширину пика на частоте сигнала, порождают боковые лепестки, которые изменяют амплитуду и положение соседних спектральных пиков, а также маскируют присутствие слабых гармонических компонент. Эффект утечки может быть ослаблен увеличением частоты отсчетов, поскольку в этом случае увеличивается спектральное разрешение, т.е. число спектральных линий, приходящихся на единицу частотного интервала. Кроме того, если разрывы на концах временного ряда предварительно сгладить, то можно уменьшить колебания спектральной функции. Это сглаживание разрывностей достигается умножением временного ряда $x(i)$ на подходящую функцию $w(i)$ во временной области:

$$x_w(i)=x(i)w(i).$$ (П53)

Функция $w(i)$ называется временным окном. Согласно теореме о свертке, умножению функций во временной  области  соответствует свертка спектральной функции $X(f)$ со спектральным окном $W(f)$ в области частот:

$$X_W(f)=X(f)*W(f).$$ (П54)

В дискретном случае прямоугольное окно выделяет из бесконечной последовательности временной ряд $x(i)$ длины $N$ и это окно во временной и спектральной областях имеет вид соответственно:

$$w_r(i) = \left\{ \begin{array}{cc} 1, & 0\le i \le N-1,\\ 0, & i < 0,~ i>N-1 , \end{array}\right.$$

$$W_r(f) = T e^{-j 2\pi f T (N-1)}\frac{\sin(\pi f TN)}{\sin(\pi f T)}.$$ (П55)

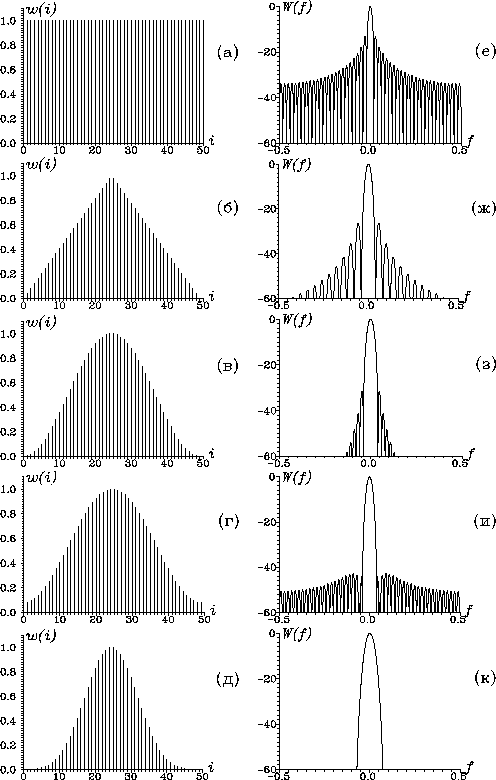
В табл. 2^П1 и на рис. 12 приведены применяемые на практике дискретно-временные окна, спектральные параметры которых выражены через спектральное представление прямоугольного окна. Для сравнения эффективности применения того или иного временного окна используется несколько показателей, представленных в табл. 3. Ширина полосы частот главного лепестка характеризует частотное разрешение. Для ее количественной оценки используют два показателя: $B_w$ и $B_e$; $B_w$ -- ширина полосы на уровне половинной энергии, т.е. на уровне, находящемся на 3 дБ ниже максимума главного лепестка; $B_e$ -- эквивалентная ширина полосы, определяемая соотношением:

$$\begin{eqnarray*} B_e=\int_{-1/(2T)}^{1/(2T)}\frac{X(0)}{X_w(f)}df. \end{eqnarray*}$$

Величины $B_w$ и $B_e$ дополнительно нормируются на частотное разрешение дискретного преобразования Фурье $\Delta f=1/(NT)$. Еще два показателя используются для оценки характеристик боковых лепестков. Один из них -- максимальный уровень боковых лепестков, который позволяет судить, насколько окно подавляет просачивание. Второй показатель -- асимптотическая скорость спадания уровня боковых лепестков от максимума к максимуму при увеличении числа отсчетов $N$. Все показатели выражаются в децибелах.

Таблица 2

Название окна	Временное представление $w(i)$	Спектральная характеристика $W(f)$
Прямоугольное	$w_r(i)$	$W_r(f)$
Треугольное (окно Барлетта)	$1 -2 \vert t(i)\vert$	$(2/N)W^2_r(f/2)$
Косинус-квадратное (окно Ханна)	$\cos^2(\pi t(i))$	$0.5W_r(f)+0.25W_r(f-\Delta f)$ $+0.25W_r(f+\Delta f)$
Приподнятый косинус (окно Хемминга)	$0.54 +0.46 \cos(2\pi t(i))$	$0.54W_r(f)+0.23W_r(f-\Delta f)$ $+0.23W_r(f+\Delta f)$
Взвешенные косинусы (окно Наттолла, $R=3$)	$\sum_{r=0}^{R}a_r\cos(2\pi rt(i))$, где $a_r$ -- параметры	$\sum_{r=0}^{R}0.5 a_r(W_r(f-r\Delta f)+W_r(f+r \Delta f))$

: Рис. 12. Дискретно-временное ( а, б, в, г, д) и спектральное ( е, ж, з, и, к) представления окон:  прямоугольного ( а, е),  треугольного ( б, ж),  Ханна ( в, з),  Хемминга ( г, и), Наттолла ( д, к).

: Рис. 13. Примеры использования оконных функций для улучшения спектрального разрешения в различных ситуациях: ( а) -- одна сильная гармоническая компонента расположена рядом со слабой компонентой, а вторая сильная компонента расположена на удалении от слабой; ( б) -- одна сильная компонента удалена от слабой; ( в) -- две компоненты расположены рядом друг с другом.

Из приведенных в табл. 3 и на рис. 12 окон самый узкий главный лепесток имеет частотная характеристика прямоугольного окна, однако у нее самый высокий уровень боковых лепестков. Окно Наттолла имеет минимальный из всех окон уровень боковых лепестков, но самый широкий главный лепесток.

Итак, применение временных оконных функций путем умножения временного ряда на оконную функцию перед операцией преобразования Фурье позволяет снизить уровень боковых лепестков по сравнению с тем их уровнем, который они имели в случае прямоугольного окна. Снижение уровня боковых лепестков уменьшает смещение соседних спектральных пиков. Однако это дается ценой расширения главного лепестка, что, естественно, приводит к ухудшению спектрального разрешения. Следовательно, необходимо находить компромисс между шириной главного лепестка и уровнем подавлением боковых лепестков.

Таблица 3

Название окна	Ширина главного лепестка по уровню половинной энергии, $B_w$	Эквивалентная ширина главного лепестка, $B_e$	Максимальный уровень боковых лепестков, дБ	Асимптоти- ческая скорость спадания боковых лепестков, дБ
Прямоугольное	0.89	1.00	-13.3	-6
Треугольное	1.28	1.33	-26.5	-12
Ханна	1.44	1.50	-31.5	-18
Хемминга	1.30	1.36	-43	-6
Наттолла	1.70	1.80	-98	-6

Например, если достаточно сильные (по амплитуде) гармонические компоненты временного ряда расположены вблизи и на отдалении от слабой компоненты ряда, то следует выбирать окно с одинаковым уровнем боковых лепестков около главного лепестка для того, чтобы обеспечить малое смещение слабой компоненты (рис. 13,  а). Если же имеется одна сильная компонента, которая удалена от слабой, то следует выбирать окно с быстро спадающим уровнем боковых лепестков, причем их уровень около главного лепестка в данном случае не имеет большого значения (рис. 13,  б). В том случае, если необходимо обеспечить высокое разрешение между близкими компонентами, а удаленные компоненты отсутствуют, то вполне приемлемым может оказаться окно с увеличивающимся уровнем боковых лепестков, но с очень узким главным лепестком (рис. 13,  в). Если спектр временного ряда относительно гладок, то можно вообще не применять окна. Иногда во временной ряд добавляют случайную компоненту, которая формирует фон из боковых лепестков на некотором уровне и, таким образом, позволяет отчетливо увидеть главные лепестки.