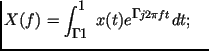 |
(П33) |
Прямое преобразование Фурье имеет вид:
Обратное преобразование Фурье записывается в виде:
С преобразованием Фурье тесно связано понятие дельта-функции ![]() (функции Дирака). Это функция, график которой имеет бесконечную
высоту, нулевую ширину и площадь, равную единице. Математическое
определение дельта-функции имеет вид:
(функции Дирака). Это функция, график которой имеет бесконечную
высоту, нулевую ширину и площадь, равную единице. Математическое
определение дельта-функции имеет вид:
Найдем обратное преобразование Фурье функции ![]() :
:
Аналогично найдем обратное преобразование Фурье функции
![]() :
:
Среди всех известных и часто применяемых на практике функций особую роль при решении задачи анализа временного ряда играют гармонические функции и так называемый прямоугольный импульс. Найдем их преобразования Фурье П1.
1. Преобразование Фурье гармонического сигнала
Непосредственно из равенств (1.38)-(1.40) можно
определить преобразования Фурье гармонических функций
![]() и
и
![]() . С этой целью сложим соотношения
(1.38) и (1.40) с одновременным умножением на
. С этой целью сложим соотношения
(1.38) и (1.40) с одновременным умножением на ![]() :
:
Таким образом, преобразование Фурье косинуса (рис. 8) есть
сумма двух дельта-функций
![]() и
и
![]() ,
каждая из которых берется со множителем
,
каждая из которых берется со множителем ![]() . Это означает, что
косинус во временной области переходит в сумму двух дельта-функций в
области частот, причем дельта-функции расположены на
частотной оси в точках
. Это означает, что
косинус во временной области переходит в сумму двух дельта-функций в
области частот, причем дельта-функции расположены на
частотной оси в точках ![]() , соответствующих частоте косинуса
, соответствующих частоте косинуса
![]() . Отсюда следует, что вся информация о функции
. Отсюда следует, что вся информация о функции
![]() после преобразования в область частот сконцентрирована в частотах
после преобразования в область частот сконцентрирована в частотах ![]() Гц.
Гц.
Преобразование Фурье функции
![]() имеет вид:
имеет вид:
2. Преобразование Фурье прямоугольного импульса
Прямоугольный импульс и его преобразование Фурье будем обозначать
![]() и
и ![]() , соответственно.
, соответственно.
Функция ![]() имеет вид (рис. 9, а):
имеет вид (рис. 9, а):
Получим преобразование Фурье этой функции:
Таким образом, преобразование Фурье прямоугольного импульса
представляет собой симметричную относительно оси ординат функцию,
максимум которой достигается на частоте ![]() . График этой функции
представлен на рис. 9, б. Видно, что ширина центрального
выступа равна
. График этой функции
представлен на рис. 9, б. Видно, что ширина центрального
выступа равна ![]() . Это означает, что ширина в области частот обратно
пропорциональна ширине во временной области.
. Это означает, что ширина в области частот обратно
пропорциональна ширине во временной области.
Прямоугольный импульс играет важную роль при решении задач анализа временных
рядов: с помощью этой функции осуществляется моделирование
реализации случайного процесса конечной длины.
Укажем два важных свойства преобразования Фурье, которые используются при работе с выборочными данными.
Свойство 1. Если имеются две
функции ![]() и
и ![]() , то их произведение
, то их произведение ![]() при
преобразовании Фурье переходит в интеграл, который называется
сверткой и имеет вид:
при
преобразовании Фурье переходит в интеграл, который называется
сверткой и имеет вид:
Свойство 2.