П1.6 Ковариационные и корреляционные функции.
Коэффициент корреляции

Определение. Ковариацией случайных величин $X$ и $Y$, которые соответственно могут принимать значения $x$ и $y$, называется интеграл

$$\begin{eqnarray*}R= E[X Y]=\int ^{\infty }_{-\infty }\int ^{\infty }_{-\infty } xyp(x,y)dxdy. \end{eqnarray*}$$

Если средние значения случайных величин отличны от нуля, то вычисления удобнее проводить, предварительно перейдя к центрированным случайным величинам. В этом случае пользуются понятием корреляции.

Определение. Корреляцией двух центрированных случайных величин ($X-E[X]$) и ($Y-E[Y]$) называется интеграл

$$\begin{eqnarray*} C= E[(X-E[X])(Y-E[Y])]=\int ^{\infty }_{-\infty }\int ^{\infty }_{-\infty } (x-\mu_x)(y-\mu_y) p(x,y)dxdy. \end{eqnarray*}$$

Корреляция (или ковариация) двух случайных величин показывает степень линейной зависимости этих величин друг от друга. На практике, как правило, перед началом вычисления характеристик временных рядов производится процедура приведения временного ряда к нулевому среднему значению. При нулевых средних понятия ковариации и корреляции совпадают. С практической точки зрения отличие этих характеристик лишь в том, что ковариация содержит полную информацию о средней энергии процесса^П1, тогда как корреляция теряет часть информации при удалении среднего значения.

Если в качестве случайных величин выбрать два значения одного процесса в различные моменты времени, то эти значения будут сильно коррелированы, когда моменты времени очень близки друг к другу, поскольку случайная величина не может за короткое время существенно измениться. Корреляция между двумя величинами в далеко отстоящие друг от друга моменты времени мала, так как за такое время случайные величины могут претерпевать практически любые изменения.

Для случайных процессов вводят понятия корреляционных и ковариационных функций, аргументом которых в случае стационарных СП является временной интервал $\tau$, разделяющий два выборочных значения случайных процессов. Если случайные величины являются значениями одного и того же СП, например, процесса $X(t)$, то указанная функция называется автоковариационной (или просто ковариационной); она рассчитывается по формуле:

$$R_{xx}(\tau )=E[X_1 X_2]= \int ^{\infty }_{-\infty }\int ^{\infty }_{-\infty } x_1x_2 p(x_1, x_2,\tau )dx_1dx_2$$ (П13)

и характеризует меру статистической зависимости значений $X_1=X(t)$ и $X_2=X(t+\tau)$, сдвинутых относительно друг друга на интервал времени $\tau$. Величина временного сдвига $\tau$ может быть как положительной, так и отрицательной, и меняется в пределах $-\infty < \tau < \infty$.

Аналогично  автокорреляционная  (или просто корреляционная) функция СП $X(t)$ имеет вид:

$$C_{xx}(\tau ) = E[(X_1-E[X])(X_2-E[X])]=$$

$$= \int ^{\infty }_{-\infty }\int ^{\infty }_{-\infty } (x_1-\mu_x)(x_2-\mu_x) p(x_1, x_2, \tau )dx_1dx_2.$$ (П14)

Если же случайные величины принадлежат разным случайным процессам, например, $X(t)$ и $Y(t)$, то функции называются взаимными ковариационной и корреляционной, рассчитываются по формулам:

$$R_{xy}(\tau ) = E[X(t) Y(t+\tau)]= \int ^{\infty }_{-\infty }\int ^{\infty }_{-\infty } xy p(x,y,\tau )dxdy,$$ (П15)

$$C_{xy}(\tau ) = E[(X(t)-E[X])(Y(t+\tau)-E[Y])]=$$

$$= \int ^{\infty }_{-\infty }\int ^{\infty }_{-\infty } (x-\mu_x)(y-\mu_y) p(x, y, \tau )dxdy$$ (П16)

и характеризуют степень связанности (взаимозависимости) двух СП $X(t)$ и $Y(t+\tau)$ в зависимости от временного сдвига $\tau$.

В случае эргодических СП авто- и взаимные ковариационные и корреляционные функции можно вычислить по одной реализации случайного процесса следующим образом:

$$R_{xx}(\tau ) = \lim_{T\rightarrow \infty}\frac{1}{2T} \int^{T}_{-T} x(t)x(t+\tau)dt = \langle x(t)x(t+\tau) \rangle ,$$ (П17)

$$R_{xy}(\tau ) = \lim_{T\rightarrow \infty}\frac{1}{2T} \int^{T}_{-T} x(t)y(t+\tau) dt = \langle x(t)y(t+\tau) \rangle ,$$ (П18)

$$C_{xx}(\tau ) = \langle (x(t)- \langle x \rangle )(x(t+\tau)- \langle x \rangle ) \rangle ,$$ (П19)

$$C_{xy}(\tau ) = \langle (x(t)- \langle x \rangle )(y(t+\tau)- \langle y \rangle ) \rangle .$$ (П20)

Перечислим основные свойства авто- и взаимных ковариационных и корреляционных функций.

Свойства авто- ковариационных и корреляционных функций

1. Ковариационная функция для значения $\tau =0$ равна среднему квадрату, или средней энергии случайного процесса^П1: $R_{xx}(0)= \langle x^2 \rangle$. Корреляционная функция  при $\tau =0$  определяет  дисперсию  СП: $C_{xx}(0)=\sigma^2_x$.

2. Ковариационная и корреляционная функции являются четными относительно $\tau$: $R_{xx}(\tau)=R_{xx}(-\tau)$, $C_{xx}(\tau)=C_{xx}(-\tau)$. Это означает, что можно рассчитывать функцию только для положительных $\tau$, а результат для отрицательных значений определить на основании свойства симметрии.

3. Ковариационная и корреляционная функции для любых $\tau$ не превосходят значений функций при $\tau =0$:

$$\vert R_{xx}(\tau)\vert\le R_{xx}(0)~~~ \mbox{и}~~~ \vert C_{xx}(\tau)\vert\le C_{xx}(0).$$

4. Если $X(t)$ является периодическим СП (содержит периодическую составляющую), то $R_{xx}(\tau)$ и $C_{xx}(\tau)$ будут периодическими функциями с таким же периодом. Это свойство может быть распространено на случайные процессы, содержащие любое количество периодических составляющих. Можно сформулировать более общее утверждение: если каждая из реализаций $x(t)$ СП $X(t)$ является периодической функцией, то автоковариационная и автокорреляционная функции будут также периодическими.

5. Если СП $X(t)$ не содержит периодических компонент, то

$$\begin{eqnarray*} \lim_{\vert\tau\vert\rightarrow \infty }R_{xx}(\tau)=\langle x... ...2, \ \ \ \lim_{\vert\tau\vert\rightarrow \infty }C_{xx}(\tau)=0. \end{eqnarray*}$$

Подобные СП называют процессами с перемешиванием, поскольку при больших значениях $\tau$ величины $X(t)$ и $X(t+\tau)$ становятся статистически независимыми.

Свойства взаимных ковариационных и корреляционных функций

1. Для пары случайных процессов $X(t)$ и $Y(t)$ можно построить две, в общем случае отличающиеся друг от друга взаимные ковариационные функции $R_{xy}(\tau)$ и $R_{yx}(\tau)$, а также две взаимные корреляционные функции $C_{xy}(\tau)$ и $C_{yx}(\tau)$, т.е. при вычислении взаимных функций важен порядок индексов.

2. Значения взаимных ковариационных и корреляционных функций при $\tau =0$ не имеют энергетической интерпретации, тем не менее, для них справедливы равенства: $R_{xy}(0)=R_{yx}(0)$ и $C_{xy}(0)=C_{yx}(0)$.

3. Взаимные ковариационные и корреляционные функции не обязательно должны иметь максимум при $\tau =0$, но всегда выполняются следующие соотношения:

$$\vert R_{xy}(\tau)\vert^2\le R_{xy}(0)R_{yx}(0) ~~~\mbox{и}~~~ \vert C_{xy}(\tau)\vert^2\le C_{xy}(0)C_{yx}(0),$$

которые справедливы для любых $\tau$. Это означает, что максимумы взаимных ковариационной и корреляционной функций могут оказаться при каком угодно $\tau$, но не могут превысить значений $\sqrt{R_{xy}(0)R_{yx}(0)}$ и $\sqrt{C_{xy}(0)C_{yx}(0)}$ соответственно.

4. Если два случайных процесса $X(t)$ и $Y(t)$ статистически независимы, то для любого интервала времени $\tau$ выполняются равенства:

$$R_{xy}(\tau)=R_{yx}(\tau)=\langle x \rangle \langle y \rangle , C_{xy}(\tau)=C_{yx}(\tau)=0.$$

Если среднее значение либо одного, либо обоих независимых СП равно нулю, то взаимная ковариационная функция равна нулю. Отметим, что из факта равенства нулю взаимных ковариационной и корреляционной функций не следует статистическая независимость СП, кроме случая, когда случайные процессы характеризуются совместной гауссовой плотностью распределения.

5. В общем случае взаимные ковариационные и корреляционные функции не являются четными относительно $\tau$. Тем не менее, для них существует вид симметрии, описываемый соотношениями:

$$\begin{eqnarray*} R_{xy}(\tau)=R_{yx}(-\tau), ~~~~~~C_{xy}(\tau)=C_{yx}(-\tau). \end{eqnarray*}$$

Эти соотношения отражают тот факт, что сдвиг СП $Y(t)$ во времени в определенном направлении эквивалентен сдвигу СП $X(t)$ в противоположном направлении.

Укажем еще одно замечательное свойство ковариационных функций, которое нам понадобится в дальнейшем: ковариационная функция суммы СП равна сумме ковариационных функций каждого СП плюс сумма всех взаимных ковариационных функций:

$$R_{(x+y)(x+y)}(\tau )= R_{xx}(\tau )+R_{yy}(\tau )+ R_{xy}(\tau )+ R_{yx}(\tau ).$$ (П21)

Аналогичное свойство выполняется для корреляционных функций.

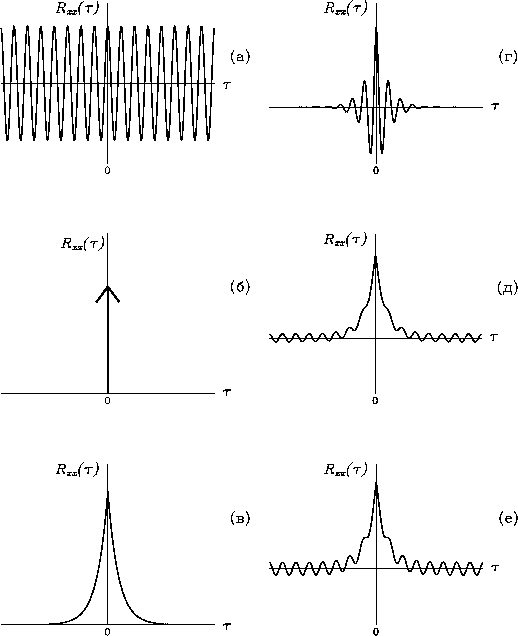
Примеры. На рис. 7 показаны вычисленные теоретически ковариационные функции процессов, с которыми часто приходится иметь дело на практике.

: Рис. 7. Ковариационные функции гармонического сигнала со случайной начальной фазой ( а), белого шума ( б), цветного шума ( в), узкополосного шума ( г), суммы гармонического сигнала со случайной начальной фазой и цветного шума ( д), суммы гармонического сигнала со случайной начальной фазой и узкополосного шума ( е). Здесь и далее стрелка на рис. (в данном случае на рис. б) соответствует дельта-функции.

Ковариационные функции используются не только для характеристики степени статистической зависимости процессов, но также с целью выявления периодичностей, выделения сигнала из шума, измерения времен запаздывания и скоростей распространения сигналов, локализации источников помех. Приведем два примера.

Пример 1. В качестве первого примера рассмотрим применение взаимных ковариационных функций для выделения слабого сигнала на фоне сильных помех. Пусть на вход некоторой системы подается два стационарных случайных процесса $X(t)$ и $Y(t)$. Эти сигналы аддитивно смешиваются и образуют на входе системы СП

$$Z(t)=X(t)+Y(t).$$

Пусть $X(t)$ -- гармонический сигнал со случайной начальной фазой (.1), а $Y(t)$ -- цветной шум (см. Приложение), статистически независимый от СП $X(t)$.

Рассчитаем автоковариационную функцию аддитивной смеси двух сигналов, применяя свойство (1.21)

$$\begin{eqnarray*} R_{zz}(\tau )= R_{xx}(\tau )+R_{yy}(\tau )+ R_{xy}(\tau )+ R_{yx}(\tau ) \end{eqnarray*}$$

и формулы (.3), (.11).

Поскольку процессы $X(t)$ и $Y(t)$ статистически независимы, то их взаимные   ковариационные   функции   равны нулю: $R_{xy}(\tau )=0$, $R_{yx}(\tau )=0$. Отсюда следует

$$R_{zz}(\tau )= \frac {A^2}{2}\cos \omega \tau +\sigma_c^2 e^{(-\alpha \vert \tau \vert )}.$$ (П22)

Средние энергии CП $X(t)$ и $Y(t)$ определяются соответственно выражениями (см. свойство 1 автоковариационной функции):

$$\begin{eqnarray*} R_{xx}(0 )= \frac{A^2}{2},~~~ R_{yy}(0)=\sigma_c^2. \end{eqnarray*}$$

Если средняя энергия шума $R_{yy}(0)$ намного больше средней энергии сигнала $R_{xx}(0)$, т.е. $\sigma_c^2 \gg A^2/2$, то график функции (1.22) имеет вид, показанный на рис. 7,  д.

Видно, что для больших $\tau$ автоковариационная функция зависит, в основном, от величины сигнала, поскольку автоковариационная функция шума стремится к нулю при $\tau \rightarrow \infty$. Таким образом, если использовать подходящий метод измерения автоковариационной функции принимаемой смеси сигналов, возникает возможность выделять эти слабые синусоидальные сигналы.

Пример 2. В радиолокации расчет ковариационных функций можно использовать для определения расстояний до цели. Пусть с помощью радиолокационной системы передается сигнал $X(t)$. Принимаемый отраженный от цели сигнал $X(t-\tau_1)$ представляет собой намного меньшую по энергии копию сигнала $X(t)$ с задержкой $\tau_1$, равной времени распространения до цели и обратно. Поскольку на входе радиолокационного приемника всегда присутствует шум, результирующее принимаемое сообщение $Y(t)$ можно представить следующим образом:

$$\begin{eqnarray*} Y(t)= AX(t-\tau_1)+N(t), \end{eqnarray*}$$

где $A$ -- постоянная, $A\ll 1$, $N(t)$ -- шум приемника.

Взаимная ковариационная функция переданного сигнала и сигнала на входе приемника равна:

$$R_{xy}(\tau ) = E[X(t) Y(t+\tau)]= E[AX(t)X(t+\tau-\tau_1)+X(t)N(t+\tau)] =$$

$$~ = AR_{xx}(\tau -\tau _1)+R_{xN}(\tau ).$$ (П23)

Так как сигнал и шум статистически независимы, то $R_{xN}(\tau )=0$ и (1.23) преобразуется к виду: $R_{xy}(\tau )= AR_{xx}(\tau -\tau _1)$.

Поскольку максимум всех автоковариационных функций приходится на начало отсчета времени (свойство 3, рис. 7), при подстройке $\tau$ таким образом, чтобы измеряемое значение $R_{xy}(\tau)$ стало максимальным, можно получить время $\tau =\tau _1$, и это время определит расстояние до цели.

Для количественной оценки степени взаимосвязи между значениями реализации удобнее рассматривать нормированные аналоги ковариационных и корреляционных функций:

$$\rho_{xx}(\tau ) = \frac{R_{xx}(\tau)}{R_{xx}(0)}= \frac{R_{xx}(\tau)}{ \langle x^2\rangle,},$$ (П24)

$$c_{xx}(\tau ) = \frac{C_{xx}(\tau)}{C_{xx}(0)}= \frac{C_{xx}(\tau)}{\sigma^2_x},$$ (П25)

которые называются коэффициентами ковариации и корреляции, соответственно. Аналогичные величины для взаимных ковариационной и корреляционной функций называются коэффициентами взаимной ковариации и взаимной корреляции, соответственно, и определяются следующими выражениями:

$$\rho_{xy}(\tau ) = \frac{R_{xy}(\tau)}{\sqrt{R_{xx}(0)R_{yy}(0)}},$$ (П26)

$$c_{xy}(\tau ) = \frac{C_{xx}(\tau)}{\sigma^2_x \sigma^2_y}.$$ (П27)

Из рассмотренных выше свойств авто- и взаимных ковариационных и корреляционных функций следует, что коэффициенты (1.24)-(1.27) могут принимать значения от $-1$ до $+1$. Тождественное равенство коэффициентов единице указывает на полное совпадение рассматриваемых процессов. Отрицательные значения коэффициентов указывают на противоположность знаков процессов. Этот вывод не всегда корректен для ковариационных функций, которые учитывают средние значения процессов и поэтому сдвигают нулевую отметку для коэффициентов ковариаций. По этой причине на практике используют, в основном, коэффициенты корреляции. Коэффициент взаимной корреляции принимает одно из граничных значений ($\pm 1$) только при наличии идеальной линейной связи между процессами. Нелинейная связь и (или) разброс данных, вызванный ошибками измерения или неполной коррелированностью процессов, приводит к уменьшению значения $c_{xy}$.