П2.2 Эффекты, обусловленные конечной длиной реализации

Пусть имеется реализация случайного процесса $x(t)$, определенная на бесконечном интервале времени $-\infty <t<\infty$ и пусть преобразование Фурье $X(f)$ этой функции известно. На практике исследователь имеет дело с реализациями конечной длины. Моделирование СП конечной длины осуществляется, как было отмечено, при помощи прямоугольного импульса, преобразование Фурье $U(f)$ которого имеет вид (1.43). Для перехода к реализации конечной длины необходимо умножить функцию $x(t)$ на прямоугольный импульс $u(t)$, ширина которого определяется временем наблюдения, при этом произойдет сужение функции $x(t)$ на интервал, равный длине выборки:

$$\begin{eqnarray*} x_P(t)=x(t)u(t). \end{eqnarray*}$$

Таким образом, после умножения $x(t)$ на прямоугольный импульс получилась функция $x_P(t)$, которая равна нулю вне интервала наблюдения $-P/2\le t \le P/2$. Это означает, что функция $x_P$ отвечает выборке длины $P$.

Преобразование Фурье  функции  $x_P(t)$, согласно свойству (1.44), представляет собой свертку:

$$X_P(f)=\int _{-\infty}^{\infty} X(\eta)U(f-\eta )d\eta = \int _{-\infty}^{\infty} X(\eta)\frac{\sin (\pi (f-\eta)P)}{\pi (f-\eta )}d\eta =$$

$$=\int _{-\infty}^{\infty} X(f-\eta)\frac{\sin (\pi \eta P)}{\pi \eta }d\eta .$$ (П46)

По существу, переход к конечной реализации СП сводится к свертке преобразований Фурье  исходного  бесконечного  сигнала  и функции $(\sin x)/x$. Продемонстрируем эффекты, которые возникают при таком переходе, на примере гармонического сигнала.

Пусть гармоническая функция имеет частоту $f_0$ и единичную амплитуду: $x(t)=\cos (2\pi f_0 t)$. Мы нашли, что преобразование Фурье косинуса на бесконечном временном интервале представляет собой сумму двух дельта-функций:

$$X(f)=\frac {1}{2}[ \delta (f-f_0)+\delta (f+f_0)] .$$ (П47)

Для сигнала конечной длины в соответствии с формулой (1.46) получим следующее преобразование Фурье:

$$X_P(f)=\int _{-\infty}^{\infty} \frac{1}{2} [ \delta (\eta-f_0)+ \delta (\eta+f_0)] \frac {\sin (\pi(f-\eta)P)}{\pi (f-\eta )}d\eta =$$

$$=\frac {\sin (\pi(f-f_0)P)}{2\pi (f-f_0)}+\frac {\sin (\pi(f+f_0)P)}{2\pi (f+f_0)}.$$ (П48)

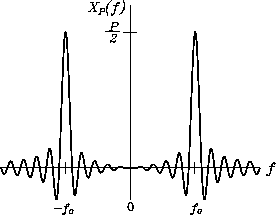
На рис. 8 и рис. 10 изображены преобразования Фурье функции $\cos (2\pi f_0 t)$ на бесконечном  и конечном  интервалах,  соответственно. Можно видеть следующее.

1. Преобразование Фурье гармонической функции на конечном интервале времени представляется суммой двух функций $(\sin x)/x$ в то время, как отображением в области частот той же гармонической функции на бесконечном интервале являлись два дельта-пика на частотах $\pm f_0$. Тем не менее максимумы функций $(\sin x)/x$ располагаются около частот $\pm f_0$. Это означает, что б $\acute {\rm о}$льшая часть информации о косинусе конечной длины концентрируется вблизи частот $\pm f_0$. Функция $X_P(f)$ нигде не обращается в нуль, за исключением самых крайних точек. Это приводит к размыванию информации по всей области частот. Итак, использование конечной длины записи во всяком реальном эксперименте позволяет получить лишь размытую в частотной области информацию.

2. Высота центрального выступа функции $(\sin x)/x$ равна $P/2$, а ширина $2/P$. Это означает, что если запись сделать длиннее, т.е. увеличить $P$, то высота главных выступов увеличится, а ширина уменьшится и, следовательно, в пределе бесконечно длинной реализации центральный выступ будет трансформироваться в дельта-пик.

: Рис. 10. Преобразование Фурье гармонической функции косинус, определенной на конечном интервале времени.

С конечной длиной записи связан еще один эффект, который заключается в невозможности точного измерения частоты. Поскольку преобразование Фурье представляется суммой двух функций $(\sin x)/x$, то вследствие наличия осциллирующих хвостов у каждой из функций максимумы $X_P(f)$ смещены относительно частот $f=\pm f_0$. Следовательно, точно оценить частоту по конечной выборке гармонического сигнала нельзя. Отметим, что более высокие частоты определить легче, т. к. взаимное влияние двух функций $(\sin x)/x$ при их отдалении друг от друга уменьшается.