 |
Рассмотрим общую схему анализа совокупности стационарных реализаций. Если реализации принадлежат нестационарным процессам, то схема анализа определяется в основном исследователем, поскольку отсутствует общепринятая методика анализа нестационарных данных. Общей рекомендацией при анализе нестационарного временного ряда является применение процедуры разделения ряда на стационарную и нестационарную компоненты с последующим анализом этих компонент в отдельности.
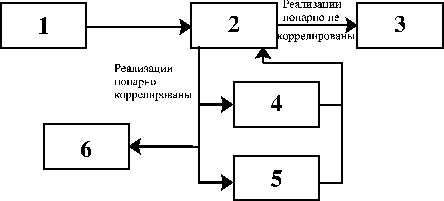
Процедура оценивания основных свойств ансамбля стационарных реализаций
СП включает, как правило, этапы, показанные на рис. 28. Как и в
случае анализа отдельных реализаций, некоторые этапы могут быть
исключены, если в них нет необходимости.
Блок 1. Оценивание свойств отдельных реализаций случайных процессов производится по схеме, описанной в п. 3.3.1.
Блок 2. На этом этапе анализируется статистическая зависимость реализаций ансамбля, т.е. степень их взаимной корреляции. Во многих случаях задачи этого этапа решаются без вычисления и детального анализа взаимных корреляционных функций и функций когерентности. Например, если известно, что интервалы времени между измерением отдельных реализаций ансамбля велики, то можно считать эти реализации некорреливанными без дальнейшего анализа. Однако, если измерения нескольких реализаций производились одновременно, то с большой вероятностью корреляция между ними существует.
Блок 3. Если на предыдущем этапе показано, что между реализациями
отсутствует корреляция, то необходимо проверить эквивалентность
(степень совпадения) статистических характеристик некоррелированных
реализаций. С этой целью оцениваются статистические характеристики
каждой реализации и затем сравниваются между собой. Если различие между
статистическими характеристиками находится в пределах дисперсии
(ошибки) оценок, то такие реализации можно считать эквивалентными
некоррелированными и в дальнейшем проводить оценки статистических
характеристик по совокупности реализаций, а не по каждой
реализации в отдельности. В результате оценки характеристик по
анамблю реализаций обладают значительно меньшей ошибкой.
Блок 4. Вычисление оценок взаимной ковариационной и корреляционной функций, а также коэффициентов ковариации и корреляции позволяет охарактеризовать степень линейной взаимосвязи двух реализаций во временной области.
Блок 5. О линейных зависимостях между реализациями в частотной области можно судить на основе оценок взаимной спектральной плотности и функции когерентности. Эти оценки позволяют также провести физическую интерпретацию корреляций между реализациями и проанализировать частотный состав реализаций.
Блок 6. В зависимости от целей исследования вычисляются другие совместные характеристики реализаций. Такими характеристиками могут быть синхрограммы на основе преобразования Гильберта, функции взаимной информации, нелинейные функции предсказуемости и т. п. Все подобные характеристики имеют специфический характер и, как правило, направлены на решение узкой задачи, например, синхрограммы позволяют судить только о наличии или отсутствии фазовой синхронизации между двумя временными рядами.