П1.3 Предварительная обработка данных

На этапе предварительной обработки осуществляется графическое представление и описание поведения реализации СП, т.е. производится построение и изучение графика временного ряда. Графические методы анализа позволяют сделать предварительные выводы о характере процесса, которые затем могут быть проверены и уточнены с помощью расчета конкретных характеристик ряда. По графику временного ряда можно визуально определить наличие тренда и его характер. Если очевидно существование тренда, т.е. нестационарности ряда, то необходимо выделить и удалить нестационарную составляющую методами, описанными во второй главе. Степень плавности или прерывистости изменения последовательных значений ряда после удаления тренда дает возможность судить о характере и величине корреляции между соседними элементами ряда. По графику временного  ряда  можно также выявить наличие периодических составляющих.

На первый взгляд может показаться, что построение графика временного ряда -- простая задача, которая решается непосредственным применением стандартных графических программ. Однако на практике, как правило, возникают некоторые проблемы, например, из-за ограниченной разрешающей способности экранов компьютеров размеры выводимых графиков могут быть также ограничены; если анализируются очень длинные выборки, то точки на экране могут слиться в сплошную черную полосу. Наличие в графической процедуре режима увеличения ("лупы") позволяет решить эти проблемы путем изображения в более крупном масштабе выбранной части временного ряда, однако при этом оказывается трудным судить о характере поведения реализации на всем исследуемом временном интервале. Приходится распечатывать графики, соответствующие отдельным частям реализации, и состыковывать их вместе, чтобы увидеть картину поведения ряда в целом. Иногда для улучшения воспроизведения длинных реализаций используется прореживание, т.е. отображение на графике не всех, а лишь некоторых точек временного ряда. Эта процедура позволяет сохранить целостное представление ряда и полезна для обнаружения трендов.

Еще одной проблемой при построении графиков являются выбросы, т.е. значения, в несколько раз превышающие по величине большинство остальных значений ряда. Графическая программа автоматически выбирает масштаб отображения так, чтобы на экране уместились все наблюдаемые значения. Для устранения этого недостатка необходимо принудительно задавать нужные границы изменения значений временного ряда, т.е. масштаб по оси ординат, при этом резкие выбросы останутся за границами экрана.

При построении графика временного ряда точки на графике обычно соединяют отрезками прямых линий, однако в некоторых ситуациях эти линии могут вносить существенные искажения в представление о поведении реализации. Поэтому полезно построить график с линиями между точками и без них и изучить оба графика.

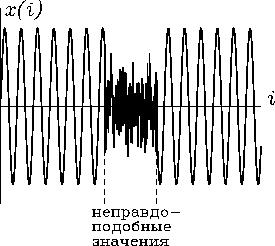
Предварительный графический анализ временного ряда позволяет определить наличие так называемых неправдоподобных значений, которые являются ложными и возникают вследствие сбоев в работе системы сбора данных. Как правило, неправдоподобные значения представляют собой изолированные точки и по величине сильно отличаются от среднего уровня временного ряда или от его характерного поведения. На рис. 26 приведен пример реализации с неправдоподобными значениями: в ходе эксперимента регистрировался периодический процесс и не было причин ожидать другого поведения реализации, поэтому наличие участка с шумоподобным поведением рассматривается как неправдоподобное. В общем случае сложно определить точно, какие данные являются неправдоподобными. Основными критериями неправдоподобности данных являются априорные сведения об исследуемом процессе и опыт исследователя. После обнаружения неправдоподобных значений они исключаются из рассмотрения.

: Рис. 26. Пример реализации с неправободобными значениями.

Во многих случаях перед оцениванием свойств реализации проводят операции приведение к нулевому среднему и единичной дисперсии.

Первая операция заключается в оценке среднего значения $\hat{\mu}_u$ ряда $u(i)$ с последующим переходом к новому временному ряду $x(i)$ с нулевым средним:

$$x(i)=u(i)-\hat{\mu}_u.$$ (П1)

Данная процедура используется при расчете практически всех характеристик реализации. Поэтому имеет смысл осуществить ее один раз, а не повторять на каждом этапе.

Вторая операция осуществляется с временным рядом $x(i)$ и состоит в оценке среднеквадратичного отклонения $\hat{\sigma}_x$ и нормировке ряда:

$$y(i)=\frac{x(i)}{\hat{\sigma}_x}.$$ (П2)

В результате нормированный ряд $y(i)$ имеет единичную дисперсию и его средняя энергия также равна единице. Переход к единичной дисперсии облегчает построение вычислительных алгоритмов и упрощает графическое изображение характеристик временного ряда, а также позволяет контролировать вычисления характеристик путем отслеживания величины средней энергии.