П1.2 Дискретизация. Ошибки маскировки частот и
квантования

Дискретизация заключается в преобразовании аналогового сигнала в цифровую форму и состоит из двух не связанных друг с другом операций: собственно дискретизации и квантования. Собственно дискретизация -- это процесс определения моментов времени, в которые должны быть произведены отсчеты; квантование -- перевод этих отсчетов в цифровую форму. Как правило, эти две операции осуществляются при помощи аналого-цифровых преобразователей (АЦП), которые связывают источник аналогового сигнала с компьютером. АЦП обычно представляют собой двоичные или двоично-десятичные системы. Двоичная система преобразует аналоговые сигналы в двоичный цифровой код, а двоично-десятичная система -- в цифровой код, который может быть представлен десятью цифрами. Конструкция двоичной системы проще, но для обработки данных на ЭВМ нужно составлять программы в машинном коде. Двоично-десятичная система сложнее, но она позволяет производить обработку данных  наблюдений  с помощью программ, написанных на обычном алгоритмическом языке.

Перевод аналогового сигнала в дискретную форму для анализа на компьютере производится, как правило, через равные промежутки времени $T$. Важно правильно выбрать величину интервала дискретизации, т.е. правильно провести операцию собственно дискретизации. Согласно теореме Котельникова, этот интервал определяется частотой Найквиста $F_n$: чтобы представление сигнала $x(t)$ в дискретной форме было однозначным, максимальный интервал дискретизации не должен превышать $T=1/(2F_n)$. Если осуществлять выборки через интервалы времени, большие $T$, то можно столкнуться с эффектом маскировки (подмены) частот, т.е. возможно перепутывание низко- и высокочастотных составляющих исходного процесса. Явление подмены является источником ошибок, которые могут возникнуть лишь при работе с выборочными данными. Если обрабатываются аналоговые сигналы, то операция дискретизации не производится и ошибки подмены не возникают.

Чтобы пояснить эффект маскировки частот, рассмотрим преобразование непрерывного сигнала, показанного на рис. 21, в дискретную форму. Интервал времени между соседними отсчетами составляет $T$ секунд. Следовательно, скорость дискретизации равна $1/T$ отсчетов в секунду. Для того чтобы выборочная функция $x(i)$ содержала все те же частоты, что и исходный непрерывный сигнал $x(t)$, на каждый цикл колебания, согласно теореме Котельникова, должно приходиться не менее двух отсчетов, а наиболее высокая частота, которая может быть выделена при дискретизации со скоростью $1/T$ отсчетов в секунду, равна частоте Найквиста $F_n$. Если в исходном сигнале содержатся более высокие частоты ($f>F_n$), то они будут свернуты в диапазон $[0, F_n]$ Гц и не будут отличимы от более низких частот этого диапазона (рис. 22). Свертывание составляющих исходного процесса относительно частоты Найквиста наглядно можно изобразить с помощью диаграммы подмен (рис. 23). На рис. 23,  а показаны исходные частоты, т.е. частоты, содержащиеся в сигнале $x(t)$. На рис. 23,  б ось частот сложена гармошкой над интервалом $[0, F_n]$ Гц кусками по $F_n$ Гц. Видно, что для любой частоты $f$ из диапазона $[0, F_n]$ Гц замаскированными под частоту $f$ являются высокие частоты $2F_n \pm f, 4F_n \pm f, \dots , 2nF_n \pm f$, где $n=1,2,\dots$.

: Рис. 21. Преобразование непрерывного сигнала в дискретную форму.

: Рис. 22. Иллюстрация эффекта подмены частоты гармонического сигнала.

: Рис. 23. Диаграмма подмены частот относительно частоты Найквиста.

Пример. Пусть имеется два непрерывных сигнала с частотами $f$ и $f_1$: $x(t)=\cos 2\pi ft$, $y(t)=\cos 2\pi f_1 t$. Если время дискретизации равно $T$, то выборочные функции $x(i)$ и $y(i)$ представятся последовательностями дискретных величин, соответствующих моментам времени $t=iT=i/(2F_n)$:

$$\begin{eqnarray*} x(i)=\cos 2\pi fiT=\cos 2\pi f\frac{i}{2F_n}=\cos \frac{\pi fi... ...i f_1 iT=\cos 2\pi f_1 \frac{i}{2F_n}=\cos \frac{\pi f_1i}{F_n}. \end{eqnarray*}$$

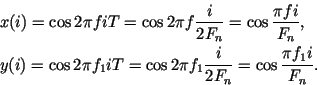
Пусть частоты $f$ и $f_1$ связаны соотношением $f_1=2nF_n \pm f$, тогда

$$\begin{eqnarray*} y(i)=\cos \pi (2nF_n \pm f) \frac {i}{F_n}=\cos (2n\pi i \pm \frac {\pi f i}{F_n}) =\cos \frac {\pi f i}{F_n}=x(i). \end{eqnarray*}$$

Таким образом, при снятии отсчетов с интервалами $1/(2F_n)$ значения косинусов с частотами $f$ и ($2nF_n \pm f$) одинаковы. Например, если $F_n =100$ Гц, то составляющие с частотой $30$ Гц будут неотличимы от составляющих с частотами $170$, $230$, $370$ Гц и т. д.

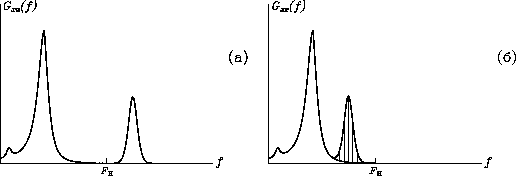
На рис. 24 показан пример расчета спектральной плотности. Если в спектре имеются частоты $f>F_n$ (рис. 24,  а), то график истинной спектральной плотности будет искажен вследствие свертывания частот (рис. 24,  б).

: Рис. 24. Спектральная плотность процесса ( а) и спектральная плотность этого же процесса, вычисленная по дискретному временному ряду с частотой дискретизации $2F_n$ ( б).

На практике при цифровом анализе данных избавиться от ошибок маскировки частот можно единственным способом. Для этого еще до процесса дискретизации необходимо подавить в исходном аналоговом сигнале ту его часть, которая может содержать частоты, превышающие частоту Найквиста. Это делают с помощью низкочастотного фильтра, который устанавливается перед аналого-цифровым преобразователем. Такие низкочастотные фильтры называются противоподменными.

Рассмотрим теперь операцию квантования, которая состоит в переводе значений сигнала из аналогового непрерывного представления в цифровую форму. Как известно, цифровое представление чисел в ЭВМ заключается в их двоичном кодировании посредством целого числа бит. Точность цифрового (машинного) представления числа в виде непрерывного множества значений определяется количеством используемых бит. В типичных преобразователях аналогового сигнала в цифровой формат для кодирования применяется от 6 до 16 бит, что соответствует диапазону от 64 до 65536 уровней квантования. Так, если для представления чисел $x$ из интервала $(0,5)$ используется 8 бит, то это означает, что весь непрерывный интервал разбит на $2^8=256$ уровней $c$, $0\le c\le 255$, с шагом квантования $\Delta x = 5/256$ и только 256 целых чисел в цифровой форме можно использовать для записи любого числа из этого интервала (рис. 25). Математически операцию квантования можно записать в виде:

$$\begin{eqnarray*}c={\rm INT}\left( \frac{x}{\Delta x} \right); \end{eqnarray*}$$

здесь INT означает округление до целой части числа. Ошибка квантования $\Delta c$ равна

$$\begin{eqnarray*} \Delta c=\frac{x}{\Delta x} - {\rm INT}\left( \frac{x}{\Delta x} \right) \end{eqnarray*}$$

и ограничена интервалом $(-0.5,0.5)$. Если преобразователь работает правильно, то ошибка квантования имеет нулевое среднее, распределена   равномерно   с  плотностью   вероятности,   равной  единице ($p(\Delta c)=1$), а дисперсия ошибки равна:

$$\begin{eqnarray*} \sigma_{\Delta c}^2=\int_{-\infty}^{\infty} (\Delta c-\mu_{\De... ...Delta c)=\int_{-0.5}^{0.5}(\Delta c)^2 d(\Delta c)=\frac{1}{12}. \end{eqnarray*}$$

Величина, обратная относительной ошибке квантования и равная отношению числа уровней квантования, используемых для представления сигнала, к величине среднеквадратичного отклонения $\sigma_c$, определяет отношение сигнал/шум данного преобразователя. Это величина обычно выражается в децибелах. Например, если для квантования используется 256 уровней, то отношение сигнал/шум составляет около 59 дБ.

: Рис. 25. Иллюстрация процесса квантования.

На практике ошибка квантования намного меньше других ошибок, возникающих в процессе сбора и обработки данных. Однако, если непрерывный входной сигнал занимает малую долю шкалы квантования, то ошибка квантования будет существенной. Поэтому всегда следует стремиться к тому, чтобы диапазон изменения значений непрерывного процесса занимал как можно большую часть шкалы квантования.

Помимо рассмотренных ошибок дискретизации и квантования укажем другие наиболее существенные ошибки, которые могут возникать в АЦП:

-- апертурная ошибка, возникающая из-за того, что каждый отсчет выполняется на протяжении некоторого отрезка времени, а не мгновенно;

-- дребезжание, являющееся следствием того, что интервал времени между соседними отсчетами может меняться случайным образом;

-- нелинейные искажения, которые могут возникать по разным причинам, например, вследствие плохой подгонки деталей системы или неточной градуировки;

-- при одновременном преобразовании в нескольких каналах наличие интервала времени между соседними опросами в различных каналах приводит к появлению межканальной временн $\acute {\rm о}$й ошибки в отсчетах, которая может оказаться существенной для быстро меняющихся сигналов. Появления этой ошибки можно избежать, если использовать в АЦП запоминающие схемы, в которые данные из всех каналов поступают одновременно и хранятся там до момента опроса соответствующего канала коммуникатором.