П2. Преобразование Гильберта

Преобразование Гильберта позволяет разложить исходный процесс на две составляющие -- амплитудную и фазовую. С простейшим примером такого разложения мы встречаемся при записи гармонической функции синуса или косинуса $x(t)=A\cos(2\pi f t+\varphi_0)$, которая характеризуется амплитудой $A$ -- максимальным отклонением от нулевого уровня, и фазой $\varphi=2\pi f t+\varphi_0$. Фаза является аргументом гармонической функции, который определяет, сколько периодов функции наблюдается от начального момента времени и каково ее значение в данный момент времени; $\varphi_0$ -- начальная фаза, т.е. фаза в момент времени $t=0$. Амплитуда гармонической функции не меняется во времени, а фаза линейно растет с коэффициентом пропорциональности $f$, который носит название частоты (рис. 16). Частота $f$ определяет число периодов (повторений значений функции) в единицу времени и является постоянной во времени величиной. Амплитуда и фаза гармонической функции отражают различную информацию: амплитуда описывает энергию, а фаза характеризует повторяемость процесса во времени, и в этом смысле они могут рассматриваться как независимые характеристики гармонической функции.

: Рис. 16. Гармоническая функция ( а) и зависимость ее фазы от времени ( б).

Негармонический процесс $x(t)$ также можно формально разложить на амплитудную и фазовую составляющие:

$$x(t)=a(t)\cos \varphi (t), ~~~ \varphi(t)=\omega(t)t+\varphi_0;$$ (П17)

здесь $a(t)$ -- амплитуда и $\varphi(t)$ -- фаза процесса $x(t)$, зависящие от времени и имеющие такой же смысл, что и для гармонической функции. Поскольку фаза зависит от времени произвольным образом, то вводится понятие мгновенной частоты $\omega(t)$:

$$\begin{eqnarray*} \omega(t)=\frac{d \varphi}{dt}=\dot \varphi. \end{eqnarray*}$$

Отметим, что для составляющих процесса (2.17) часто используются термины мгновенная амплитуда и мгновенная фаза, чтобы подчеркнуть их отличие от амплитуды и фазы гармонической функции.

Представление процесса $x(t)$ в виде (2.17) означает, что, во-первых, амплитуда, фаза и частота являются функциями времени и, следовательно, могут характеризовать нестационарный СП, и, во-вторых, исходный СП раскладывается на две составляющие -- амплитуду и фазу, поведение которых может анализироваться в отдельности.

Существует бесконечное число способов представления исходного СП в виде (2.17). Действительно, можно формально записать СП в комплексной форме: $z(t)=x(t)+j \bar{x}(t)$, дополнив реальный процесс $x(t)$ произвольной мнимой частью $\bar{x}(t)$. Тогда

$$z(t)=a(t)e^{ j \varphi (t)};$$ (П18)

здесь мгновенные амплитуда $a(t)$, фаза $\varphi(t)$ и частота $\omega(t)$ определяются выражениями:

$$a(t) = \sqrt{x^2(t)+\bar{x}^2(t)}, \ \ \ \varphi(t)=\arccos \frac{x(t)}{a(t)}=\arcsin\frac{\bar{x}(t)}{a(t)},$$

$$\omega(t) = \frac{\dot{\bar{x}}(t) x(t)-\dot x(t) \bar{x}(t)}{a^2(t)}.$$ (П19)

При такой записи амплитуда, фаза и частота процесса $x(t)$ столь же произвольны, как мнимая часть $\bar{x}(t)$. Если указать оператор, который ставит в соответствие функции $x(t)$ функцию $\bar{x}(t)$, то произвольность можно исключить. Таким оператором является преобразование Гильберта. Это преобразование обладает рядом свойств, благодаря которым при записи функций $x(t)$ и $z(t)$ информация об исходном СП не искажается.

Преобразование Гильберта действительной функции $x(t)$, определенной во всей временной области $-\infty <t<\infty$, есть действительная функция $\bar{x}(t)$, также определенная на всей временной оси и задаваемая формулой:

$$\bar{x}(t)=\int_{-\infty}^{\infty}\frac{x(\tau)}{\pi(t-\tau)}d\tau ,$$ (П20)

в которой интеграл понимается в смысле главного значения Коши. Преобразование Гильберта является линейным оператором. Для него существует обратное преобразование и выполняется свойство: энергии $\bar{x}(t)$ и $x(t)$ одинаковы, т.е. преобразование (2.20) удовлетворяет необходимым условиям для получения неискаженной информации о процессе $x(t)$.

Подчеркнем, что комплексная запись гармонической функции получается дополнением действительной функции мнимой частью, отличающейся от действительной поворотом фазы на $-\pi/2$. Преобразование Гильберта обобщает это правило на произвольные функции: если представить процесс $x(t)$ как суперпозицию гармонических функций, то мнимая часть $\bar{x}(t)$, сопряженная по Гильберту, есть суперпозиция тех же гармонических функций, сдвинутых по фазе на $-\pi/2$. Пусть $X(f)=\vert X(f)\vert e^{-j\phi_x(f)}$ является преобразованием Фурье сигнала $x(t)$, тогда сопряженную по Гильберту мнимую часть $\bar{x}(t)$ можно вычислить как обратное преобразование от $\bar{X}(f)$:

$$\bar{x}(t)=\int_{-\infty}^{\infty}\bar{X}(f)e^{-j2\pi ft}dt,$$ (П21)

в котором образ Фурье $\bar{X}(f)$ связан с фурье-образом $X(f)$ исходного сигнала выражением:

$$\bar{X}(f) = \vert\bar{X}(f)\vert e^{(-j\bar{\phi}_x(f))}= \vert X(f)\vert e^{-j[\phi_x(f)+\phi_b(f)]},~~~ \bar{X}(0)=0,$$

$$\phi_b(f) = \left\{ \begin{array}{c} \pi/2,\ \ f>0; \\ -\pi/2, \ \ f<0. \end{array}\right.$$ (П22)

Таким образом, преобразование Гильберта может быть осуществлено с помощью идеального фазовращателя, оставляющего модуль $X(f)$ неизменным и сдвигающего фазу аргумента $\phi_x(f)$ на $\pi/2$ на положительных частотах и на $-\pi/2$ на отрицательных частотах. Если осуществлять обработку информации в режиме реального времени, то такую операцию можно реализовать только приближенно, но с произвольно высокой точностью для процесса, известного на всей временной оси. Выражения (2.20)-(2.21) применимы как для периодических функций, которые записываются через ряды Фурье, так и для процессов, представляемых интегралом Фурье.

Итак, с помощью преобразования Гильберта (2.20) и выражения (2.18) мы можем поставить в соответствие действительной функции $x(t)$ комплексную функцию $z(t)$, которая носит название аналитического сигнала^П1. Преобразование Фурье аналитического сигнала с учетом выражения (2.22) записывается в виде:

$$Z(f)=X(f)+ j \bar{X}(f)=\left\{ \begin{array}{cc} 2 X(f), & f>0; \\ 0 ,& f<0, \\ X(0), & f=0. \end{array}\right.$$ (П23)

Следовательно, спектральная функция $Z(f)$ аналитического сигнала полностью определяется   спектральной  функцией  исходного  сигнала $X(f)$. Поэтому обратное преобразование Фурье $Z(f)$ даст аналитический сигнал $z(t)$, причем $\bar{x}(t)= Im [z(t)]$.

: Рис. 17. Реализации ( а, г), мгновенные амплитуды ( б, д) и мгновенные фазы ( в, е) амплитудно- и частотно-модулированных сигналов, соответственно.

: Рис. 18. Реализации ( а), мгновенные амплитуды ( б) и мгновенные фазы ( в) первой (сплошная линия) и второй (пунктирная линия) взаимосвязанных хаотических систем. Разности между реализациями ( г), мгновенными амплитудами ( д) и мгновенными фазами ( е) хаотических систем.

Зная действительную $x(t)$ и мнимую $\bar{x}(t)$ части аналитического сигнала $z(t)$, можно вычислить амплитуду $a(t)$, фазу $\varphi(t)$ и мгновенную частоту $\omega(t)$ процесса $x(t)$ с помощью выражений (2.19). На практике преобразование Гильберта временного ряда $x(i)$ конечной длины $N$ чаще всего осуществляется через аналитическую функцию по алгоритму, согласно которому необходимо

-- определить с помощью алгоритма комплексного БПФ^П1преобразование Фурье $X(f_k)$ анализируемого временного ряда;

-- вычислить фурье-образ $Z(f_k)$ аналитического сигнала с помощью выражения (2.23);

-- осуществить обратное преобразование Фурье от $Z(f_k)$ с помощью комплексного БПФ и получить аналитический сигнал $z(i)$;

-- разделить мнимую часть аналитического сигнала $z(i)$ и действительную; в результате получить искомое преобразование Гильберта $\bar{x}(i)$.

Преобразование  Гильберта  временного ряда можно  осуществить также с помощью выражения (2.20), заменяя интегрирование на суммирование:

$$\bar{x}(i)=\sum_{k=1}^{N}\frac{x(k)}{\pi(i-k)} ,$$ (П24)

где суммирование ведется по всем $k\ne i$. Однако вычисление преобразования Гильберта по приведенному алгоритму требует значительно меньших затрат вычислительных ресурсов, чем прямое вычисление через суммирование (2.24).

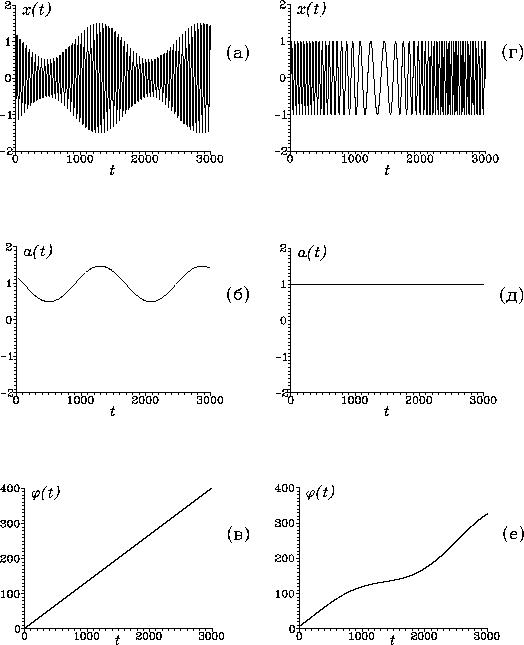
На рис. 17 приведены примеры преобразований Гильберта амплитудно- и частотно-модулированных сигналов, которые наглядно демонстрируют физический смысл преобразования -- идеальное детектирование сигналов.

Преобразование Гильберта широко используется для анализа временных рядов, особенно стохастического происхождения, и для определения степени синхронности между временными рядами, которые порождаются стохастическими и хаотическими системами. В последнем случае ряды раскладываются на амплитудную и фазовую составляющие, которые анализируются независимо. Это позволяет обнаружить взаимосвязь сигналов, проявляющуюся в синхронности динамики фаз, даже тогда, когда амплитудная динамика остается несвязанной и другие методы обнаружения связанности процессов являются непригодными.

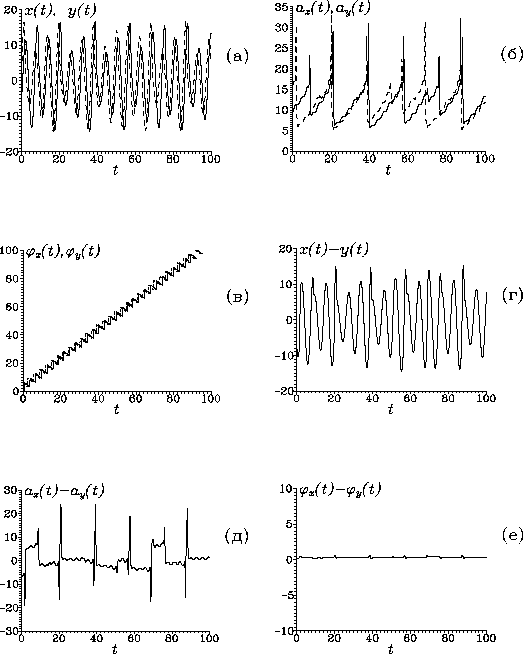
Рассмотрим применение  преобразования Гильберта для анализа синхронности между двумя взаимосвязанными хаотическими системами. На рис. 18 показаны реализации первой $x(t)$ и второй $y(t)$ хаотических систем, их мгновенные амплитуды $a_x(t)$, $a_y(t)$ и фазы $\varphi_x(t)$, $\varphi_y(t)$. Для того чтобы выяснить наличие синхронности между системами рассмотрим поведение разностей:  $x(t)-y(t)$,  $a_x(t)-a_y(t)$, $\varphi_x(t)-\varphi_y(t)$. Как видно (рис. 18), разности между реализациями систем и мгновенными амплитудами сильно изменяются во времени, а разность между мгновенными фазами практически не меняется. В этом случае говорят, что наблюдается фазовая синхронизация между системами, а их амплитудная динамика является несинхронной. Данный вывод можно сделать только благодаря использованию понятий мгновенной амплитуды и фазы и применению преобразования Гильберта.