П2.4 Дискретное преобразование Фурье

Мы ввели в рассмотрение две формы преобразования Фурье -- интегральное преобразование (1.33) и (1.36), которое определено на бесконечном интервале непрерывных значений времени и отображает непрерывную временную функцию в частотную область, и непрерывно-дискретное преобразование (1.49), которое определено на бесконечном интервале дискретных значений времени и тем самым дает возможность определять частотный состав сигнала, заданного бесконечным временным рядом. Для вычислений на ЭВМ применяется третья форма записи -- дискретное преобразование Фурье, в которой как $X(f)$, так и $x(t)$ дискретны и пределы суммирования конечны:

$$X(k)=T\sum _{i=0}^{N-1} x(i)e^{-j2\pi ik/N},~~~ x(i)=b\sum _{k=0}^{N-1} X(k)e^{j2\pi ik/N}.$$ (П50)

Дискретные значения частот в преобразовании (1.50) обусловлены конечной длиной записи, т.е. конечностью временного ряда. Здесь для краткости, как и в случае непрерывно-дискретного преобразования, вместо $x(iT)$ используется обозначение $x(i)$. Точно также вместо $X(bk)$ записано $X(k)$. Величина $b$  зависит  от  интервала  дискретизации: $b=(NT)^{-1}$.

К форме записи (1.50) можно перейти от непрерывно-дискретного преобразования Фурье (1.49), полагая $x(i)=0$ для $i<0$ и $i>(N-1)$, а также определяя дискретные значения частот следующим образом: $f_k =bk$. Покажем это.

$$\begin{eqnarray*} X(f_k)=X(bk)=X(k)&=&T\sum _{i=0}^{N-1} x(i)e^{-j2\pi f_k iT}= ... ...} X(f_k )e^{j2\pi f_k iT}= b\sum _{k=0}^{N-1} X(k)e^{j2\pi k/N}. \end{eqnarray*}$$

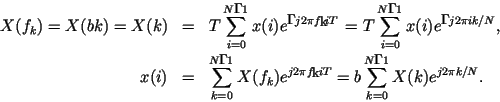
Укажем некоторые особенности дискретного преобразования Фурье, знание которых необходимо для правильного составления алгоритма вычисления на ЭВМ.

1. Согласно теореме Котельникова, максимально возможной частотой в спектре является частота Найквиста $F_n=(2T)^{-1}$, поэтому соответствующее значение $k$ в формуле (1.50) определяется из условия $f_k=F_n$:

$$\begin{eqnarray*} \frac {k}{NT}=\frac {1}{2T}~~~ {\rm или}~~~ k=\frac {N}{2}. \end{eqnarray*}$$

Отсюда следует, что частота Найквиста соответствует середине последовательности $X(k)$. Это означает, что значениям индексов $k$ в промежутке $0, \dots , N/2$ соответствуют частоты, непревосходящие частоту Найквиста. Какой же смысл имеют величины $X(k)$ при $k>N/2$? Оказывается, что этим величинам соответствуют отрицательные частоты. Покажем это. В формуле (1.50) заменим индекс $k$ на $-p$:

$$\begin{eqnarray*} X(-p)=T\sum _{i=0}^{N-1} x(i)e^{-j2\pi i(-p)/N}. \end{eqnarray*}$$

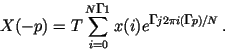
Далее умножим экспоненту на единицу, записанную в виде: $e^{-j2\pi iN/N}$:

$$\begin{eqnarray*} X(-p)&=& T\sum _{i=0}^{N-1} x(i)e^{-j2\pi i(-p)/N}e^{-j2\pi iN/N}= \\ ~&=&T\sum _{i=0}^{N-1} x(i)e^{-j2\pi i(N-p)/N}= X(N-p), \end{eqnarray*}$$

т.е. $X(-p)=X(N-p)$. Таким образом, при вычислении дискретного преобразования Фурье, подобно случаю непрерывного преобразования, в спектре с необходимостью появятся отрицательные частоты, которые однако отсутствуют в реальном спектре и появление которых и в дискретном, и в непрерывном случаях обусловлено математической операцией преобразования Фурье. Поэтому для $N$ значений данных получается примерно вдвое меньше значений спектральных составляющих.

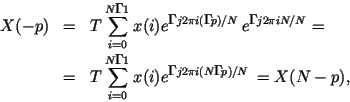
2. Дискретное преобразование Фурье является периодическим. Покажем это. Предположим, например, что $i=pN+q$; $p$, $q$ -- целые числа, причем $0\le q\le N-1$. Подставим новое значение $i$ в выражение обратного преобразования Фурье:

$$\begin{eqnarray*} x(i)=x(pN+q)&=&b\sum _{k=0}^{N-1} X(k)e^{-j2\pi k(pN+q)/N}= \\ ~&=&b\sum _{k=0}^{N-1} X(k)e^{j2\pi kq/N}e^{j2\pi kpN/N}=x(q). \end{eqnarray*}$$

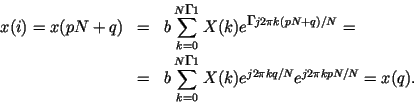
Последнее в этом выражении равенство обусловлено тем, что множитель $e^{j2\pi kpN/N}$ равен единице. Аналогичное доказательство можно провести для функции $X(k)$. Таким образом, если попытаться продолжить вычисления для индексов $k>N$, то полученные значения $X(k)$ полностью повторят уже имеющиеся: $X(k+N)=X(k)$. Поэтому для вычисления функций $x(i)$ и $X(k)$ вне множества $0, \dots, (N-1)$ следует брать значения их индексов по модулю $N$.