практикума "Анализ временных рядов":
Расчет старшего показателя Ляпунова
по временному ряду
|
|
|
|
|
|
В данной работе будет рассмотрен наиболее часто используемый на практике метод расчета ляпуновских показателей по временному ряду, предложенный в статье Вольфа с соавторами (Physica D, 1985). Этот метод немного напоминает стандартный подход к вычислению спектра ЛХП потоковых систем по известной математической модели (метод Бенеттина). В целом, техника расчета ляпуновских показателей базируется на следующей идеологии.
Предположим, что задана ![]() -мерная динамическая система с непрерывным
временем. Чтобы охарактеризовать устойчивость ее решения, анализируется
временная эволюция бесконечно малой
-мерная динамическая система с непрерывным
временем. Чтобы охарактеризовать устойчивость ее решения, анализируется
временная эволюция бесконечно малой ![]() -мерной сферы начальных условий; с
течением времени эта сфера преобразуется в эллипсоид. Если говорить о
спектре ЛХП, то
-мерной сферы начальных условий; с
течением времени эта сфера преобразуется в эллипсоид. Если говорить о
спектре ЛХП, то ![]() -й показатель Ляпунова может быть определен в терминах
длин осей эллипсоида
-й показатель Ляпунова может быть определен в терминах
длин осей эллипсоида ![]() :
:
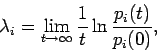
где
Отметим, что если задается только одно возмущение (это значит, что мы следим
лишь за главной осью эллипсоида), то оно будет в линейном приближении расти
по закону
![]() . Для двух независимых возмущений площадь
образуемого ими квадрата (или прямоугольника) эволюционирует по закону
. Для двух независимых возмущений площадь
образуемого ими квадрата (или прямоугольника) эволюционирует по закону
![]() ; для трех - эволюция объема описывается
законом
; для трех - эволюция объема описывается
законом
![]() и т.д. Данное свойство
приводит к несколько иному определению спектра ляпуновских экспонент: сумма
первых
и т.д. Данное свойство
приводит к несколько иному определению спектра ляпуновских экспонент: сумма
первых ![]() показателей определяется скоростью экспоненциального роста
показателей определяется скоростью экспоненциального роста
![]() -мерного элемента объема. Такая интерпретация обеспечивает основу для
техники анализа экспериментальных данных (когда требуется вычислить
несколько показателей).
-мерного элемента объема. Такая интерпретация обеспечивает основу для
техники анализа экспериментальных данных (когда требуется вычислить
несколько показателей).
Любая потоковая ДС, если ее решение отлично от состояния равновесия, имеет по крайней мере один нулевой показатель, характеризующий практически не меняющуюся величину оси эллипсоида, касательной к потоку. Оси, размер которых будет увеличиваться (уменьшаться) во времени, соответствуют положительным (отрицательным) показателям.
Иногда ляпуновские показатели анализируют в терминах информации, в
частности, как скорость потери информации о начальном состоянии. Поэтому их
порой определяют в таких единицах как bits/s (количество бит информации в
секунду), bits/period (для потоковых систем) или bits/iteration (для систем
с дискретным временем). Соответственно, вычисляют скорость разбегания
соседних траекторий не по закону
![]() , а по закону
, а по закону
![]() . Например, если старший показатель Ляпунова аттрактора
Лоренца равен 2.16 bits в единицу времени, а начальные условия определены с
точностью до одной миллионной части (
. Например, если старший показатель Ляпунова аттрактора
Лоренца равен 2.16 bits в единицу времени, а начальные условия определены с
точностью до одной миллионной части (![]() bits), то дальнейшее
поведение не может быть предсказано спустя
bits), то дальнейшее
поведение не может быть предсказано спустя ![]() единиц безразмерного
времени (20/2.16), что соответствует
единиц безразмерного
времени (20/2.16), что соответствует ![]() 20 условным периодам (оборотам
вокруг одного из состояний равновесия). Спустя это время малая начальная
неопределенность будет покрывать весь аттрактор, т.е. фазовая точка может
оказаться где угодно.
20 условным периодам (оборотам
вокруг одного из состояний равновесия). Спустя это время малая начальная
неопределенность будет покрывать весь аттрактор, т.е. фазовая точка может
оказаться где угодно.
Поскольку расчет ляпуновских экспонент по экспериментальным данным имеет
одну общую идеологию с расчетом показателей по системе ОДУ, кратко
проанализируем эту процедуру.
Как известно, для режима динамического хаоса характерно наличие экспоненциальной неустойчивости траекторий, количественной мерой которой является положительный ляпуновский показатель, характеризующий степень чувствительности системы к выбору начальных условий. Число положительных экспонент в спектре ЛХП определяется количеством неустойчивых направлений периодических орбит, встроенных в хаотических аттрактор, хотя в принципе возможны и более сложные ситуации (состоящие в сосуществовании периодических орбит с различным числом неустойчивых направлений). Мы ограничимся рассмотрением динамических систем с одним положительным показателем Ляпунова
Если уравнения ДС, генерирующей фазовую траекторию, известны, то определить величину максимального показателя (или полный спектр ЛХП) можно с помощью хорошо известного алгоритма, предложенного в работе Бенеттина с соавторами (независимо похожую технику предложили Шимада и Нагашима). Данный метод часто называют стандартным алгоритмом расчета ляпуновских экспонент.
Рассмотрим систему ОДУ:
в которой
где
Метод расчета
Мы не можем выбирать вектор возмущения при перенормировках строго в заданном
направлении, и должны брать новую точку там, где мы ее можем найти (в
некотором конусе) - рис. 2. Невозможность выбора вектора возмущения строго в
заданном направлении приводит к появлению ошибки ориентации (угол ![]() ).
Поскольку работа с одной единственной траекторией ограничивает возможности
выбора вектора возмущения, на практике приходится искать компромисс между
уменьшением ошибки его ориентации в фазовом пространстве и минимизацией его
длины. Ограничения на длину могут быть сформулированы следующим образом:
).
Поскольку работа с одной единственной траекторией ограничивает возможности
выбора вектора возмущения, на практике приходится искать компромисс между
уменьшением ошибки его ориентации в фазовом пространстве и минимизацией его
длины. Ограничения на длину могут быть сформулированы следующим образом:
Необходимо вводить минимальное значение
Несколько слов о перенормировках вектора. Здесь возможны варианты:
- перенормировки проводятся после достижения определенного расстояния между
траекториями (
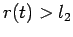 );
);
- перенормировки проводятся через фиксированные интервалы времени (например, через характерный период колебаний).
Возможны также комбинации этих двух способов осуществления перенормировок. В любом случае, выбором параметров алгоритма приходится искать компромисс: слишком частые перенормировки приводят к увеличению ошибок ориентации; слишком редкие - позволяют увеличиваться вектору возмущения, выводя за рамки линейного приближения.
Метод перенормировок при достижении фиксированного расстояния между траекториями хорошо работает для достаточно однородных аттракторов, когда зависимость от выбора точки на аттракторе не слишком сильная. Если анализируются неоднородные аттракторы, то предпочтительнее оказывается метод перенормировок через фиксированные промежутки времени.
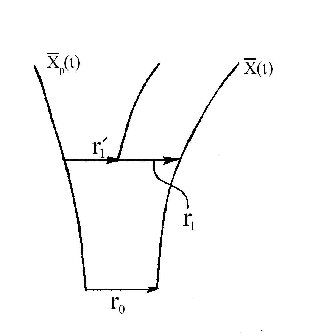
Рисунок 1 |
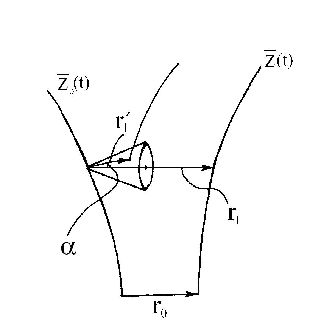
Рисунок 2 |
![]() Как написать, откомпилировать и запустить простую С-программу
Как написать, откомпилировать и запустить простую С-программу
![]() Как выводить результаты расчета на экран в виде графиков
Как выводить результаты расчета на экран в виде графиков
![]() Руководство по языку C
Руководство по языку C
![]() Использование программы gnuplot для оперативного вывода
графической информации.
Использование программы gnuplot для оперативного вывода
графической информации.
1) Ознакомление с теоретическим материалом.
2) Расчет старшего показателя Ляпунова периодического режима колебаний
и оценка точности вычислений. Исследование влияния параметров алгоритма
(задержки, величины вектора возмущения и т.д.) на
погрешность оценки показателя (задание 1).
3) Расчет старшего ляпуновского показателя хаотической динамики по
реализации предложенной преподавателем модели (задание 2).
4) Оформление отчета по полученным результатам.
Отчет по лабораторной работе представляется в виде latex или html документа по указанию преподавателя. Он должен содержать:
1) Заголовок, с указанием названия лабораторной работы, Ф.И.О. выполнявших ее студентов, номер учебной группы, номер задания.
2) Сведения (уравнения и комментарий) о модельной системе, смысл параметров, диапазон их изменения.
3) Построенную двупараметрическую бифуркационную диаграмму.
4) Информацию о количестве и типе аттракторов либо особых точек/траекторий в исследованной области и о смысле бифуркационных линий
5) Наброски фазовых портретов либо копии экрана, характеризующие поведение исследуемой системы в различных областях управляющих параметров.
6) Краткое резюме - заключение по пунктам 1-5.
Задание 1. С помощью программы ``lhp.x'' провести расчеты
старшего ляпуновского показателя периодического режима колебаний.
Построить зависимости величины ![]() от:
от:
(а) времени задержки (при фиксированных остальных параметрах);
(б) размерности пространства вложения;
(в) минимального расстояния между точками в фазовом пространстве (![]() );
);
(г) максимального расстояния между точками в фазовом пространстве (![]() );
);
(д) времени между перенормировками.
| N варианта | динамическая система | примечание |
| 1 | система Ресслера | - |
| 2 | система Лоренца | - |
| 3 | генератор с инерционной нелинейностью | - |
| 4 | модель нефрона | - |
| 5 | модель нейрона (Хиндмарш-Розе) | - |
| 6 | модель бета-клетки | - |
Задание 2. Провести те же самые расчеты для случая хаотического режима колебаний. Оценить погрешность вычислений.