Glyzin Sergey D.

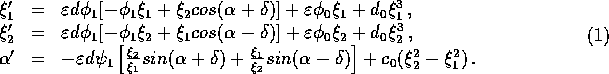
Bifurcations of the normal form of pair weakly linked oscillators
Sergey D. Glyzin
Yaroslavl State University, Yaroslavl, Russia

Two weakly linked oscillators interaction may be described by normal form

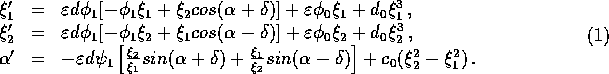
Here are amplitudes of near to harmonic oscillators and is phase difference. The parameters characterize oscillators and define linkage between them. This problem has non-trivial meaning only if . All possible bifurcations of dynamic system (1) have been defined. The decrease of linkage parameter d implies instability of synchronous regime and complicate regimes may bifurcate.

There exist wide area of parameters where the system (1) demonstrates chaotic behavior. There occurs a bifurcations cascade of strange attractors while linkage parameter d increase. It is similar to doubling period cascade. At each stage of such cascade we have:

1. Stable self-symmetrical cycle loses symmetry and bifurcates into a pair of mutually-symmetrical cycles;
2. For each of these cycles we have usual doubling period bifurcation cascade, generating a pair of chaotic mutually-symmetrical attractors;
3. These attractors are transformed into one self-symmetrical chaotic attractor;
4. It collapse into stable self-symmetrical cycle. This cycle have a period near doubled relatively to the initial cycle.

Further the process is repeated. This cascade implies the birth of chaotic attractor of higher Liapunov's dimension. Further increase of linkage parameter leads to separatrixes splitting bifurcation and chaotic attractor disappears.