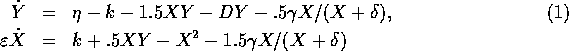
Symmetry breaking bifurcations in the chain of
inhibitory coupled
relaxation oscillators
E.I. Volkov
P.N.Lebedev Physical Institute, Leninskii pr. 53, 117924
Moscow
This report examines spatially asymmetrical collective modes in the ring of three diffusively coupled identical relaxation oscillators. The ring made from the membrane oscillators [1]
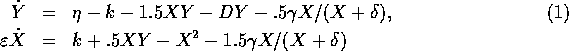
with different time scales for X (fast variable, activator) and Y (slow variable, inhibitor) was studied in details. Solely inhibitory coupling via simple linear diffusion is considered for cyclic boundary conditions.
Numerical investigations revealed the following attractors with broken symmetry:
(1) Wellknown spatially asymmetric anti-phase limit cycle whose waveforms can not be brought into coincidence by time shifts;
(2) New asymmetric version of rotating wave for stiff oscillators (small
) which are characterized by different time series for all three
oscillators.
(3) So called 'dynamical trap' - a solution in which only two oscillators are running along full cycle while the third oscillator can not generate the burst of fast variable.
Calculations of phase diagrams show that not only the existence of new attractors but the structure of phase diagrams strongly depend on the stiffness that is a characteristic feature of naturally occuring oscillators.