Exactly resolvable model of random medium
based on the stable law theory
V.V. Uchaikin and G.G. Gusarov
Moscow State University Branch in Ulyanovsk, Ulyanovsk, Russia
One of the most interesting application of statistical mechanical
concepts is the large-scale distribution of matter in the universe.
Most of its properties have been obtained by a statistical
correlation analysis for catalogs of galaxies and clusters [1,2].
The galaxies are considered as the smallest individual entities and
their distribution is characterized by points 
in the 3-dimensional Euclidian space.
The standard analysis consists in the calculation of
two - point correlation function
Observations show, that C(r) can be approximated by a power law
This fact is the basis for the assumption about of a fractal structure of the universe [2].
At first the use of walk method for mathematical simulating such distribution of galaxies was offered by Mandelbrot [3]. The process starts from choosing the position where the first galaxy to be, the next galaxy is placed in a random isotropic direction and at a random distance l from the previous one while l is chosen from the distribution
This procedure repeats many (maybe infinitely large number of) times and every time the value and direction of l are independently chosen. Based on such probability distribution the model cannot be solved exactly.
In present work it is shown that choice of 3-dimensional spherically
symmetric stable distribution 
,
having the same asymptotic behaviour as power law 
,
instead of the 
leads to exact
analytical expressions for irreducible correlation functions of
different orders and the cut off probability 1 - q at each step:
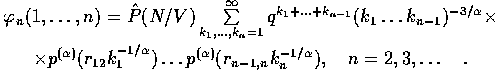
Here 
is the average number of all the particles per
unit volume, 
and 
means the summation
over all n! permutations of the arguments.
The characteristic exponent of stable law 
so the
stable distribution densities form a whole family. The distribution
is a normal (Gauss') law, 
is Cauchy's law.
Other distributions cannot be expressed in
elementary functions and are calculated and tabulated in this work.