практикума "Анализ временных рядов":
Меры сложности. Расчет энтропии источника.
К настоящему времени в научной литературе предложен целый ряд различных энтропий. Среди них энтропия источника является одной из наиболее известных и общепринятых характеристик сложности символьных последовательностей. Прежде чем давать ее определение, рассмотрим некоторые предварительные сведения.
Исторически понятие энтропии было введено Больцманом в термодинамике. В 40-х годах 20-го века концепция Больцмана была обобщена Шенноном на случай символьных последовательностей для того, чтобы иметь возможность охарактеризовать последовательность символов с точки зрения ее упорядоченности.
Предположим, что мы рассматриваем символьную последовательность,
составленную из алфавита, содержащего ![]() возможных символов.
Предположим также для простоты, что все символы являются независимыми и
равновероятными. В этом случае энтропия
возможных символов.
Предположим также для простоты, что все символы являются независимыми и
равновероятными. В этом случае энтропия ![]() интерпретируется как информация
о получении некоторого символа
интерпретируется как информация
о получении некоторого символа ![]() с вероятностью
с вероятностью ![]() . Формула для
энтропии записывается с учетом нескольких обстоятельств, а именно:
. Формула для
энтропии записывается с учетом нескольких обстоятельств, а именно:
- Допустим, что мы получаем по буквам какой-то текст. Пока мы его еще не
получили целиком, существует неопределенность о последующих символах.
Получение каждого нового символа
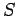 эту неопределенность уменьшает. При
этом считается, что неопределенность, которая устраняется при получении
символа
эту неопределенность уменьшает. При
этом считается, что неопределенность, которая устраняется при получении
символа 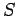 , будет тем меньше, чем больше вероятность символа (
, будет тем меньше, чем больше вероятность символа (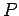 ). Редко
встречающиеся (мало ожидаемые) символы несут больше информации, чем часто
встречающиеся (более ожидаемые) символы. С точки зрения математики это
означает, что
). Редко
встречающиеся (мало ожидаемые) символы несут больше информации, чем часто
встречающиеся (более ожидаемые) символы. С точки зрения математики это
означает, что
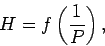
где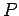 - вероятность,
- вероятность, 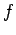 - некоторая функция, которая будет монотонно
увеличиваться с ростом
- некоторая функция, которая будет монотонно
увеличиваться с ростом 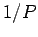 .
.
- Количество информации, которое несут
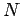 независимых символов
независимых символов 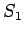 ,
, 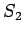 ,
,
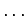 ,
, 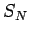 , должно определяться следующим образом:
, должно определяться следующим образом:
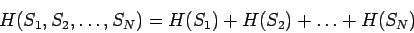
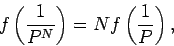
а такими свойствами обладает логарифмическая функция.
Следовательно, формула для ![]() должна иметь вид:
должна иметь вид:
Если символы не являются равновероятными, то необходимо провести усреднение
по всем возможным ![]() символам, чтобы получить величину, которая
характеризует среднюю меру неопределенности о символе (сообщении) до его
приема:
символам, чтобы получить величину, которая
характеризует среднюю меру неопределенности о символе (сообщении) до его
приема:
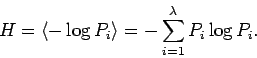
Обычно логарифмы берутся по основанию
Что может сообщить энтропия о последовательности символов? Здесь нужно обратить внимание на одно обстоятельство. Меры сложности (и, в частности, энтропия) широко применяются при анализе структуры не только текстов и ''естественных'' символьных последовательностей (таких как цепочка нуклеотидов ДНК), но и временных рядов самого различного происхождения. Часто расчет энтропии проводится в целях получения количественной характеристики сложности изучаемого процесса; при этом используется символьное представление сигналов (в простейшем случае сигнал преобразуется в бинарный код). Например, если наблюдаемая переменная в данный момент времени принимает значение больше среднего, то в качестве очередного символа бинарного кода выбирается ``1'', если меньше среднего - ``0'' и т.п. Анализ последовательностей символов вместо временного ряда осуществляется в рамках так называемой символьной динамики. В данной работе для простоты мы ограничимся только рассмотрением случая бинарных кодов.
Итак, пусть анализируется последовательность из ``0'' и ``1''; вероятности
данных символов соответственно равны ![]() и
и ![]() . Если логарифм
вычисляется по основанию 2, то энтропия будет принимать значения в
интервале от 0 до 1.
. Если логарифм
вычисляется по основанию 2, то энтропия будет принимать значения в
интервале от 0 до 1. ![]() , если вероятности одинаковы
, если вероятности одинаковы ![]() ;
; ![]() ,
если постоянно генерируется только один символ (
,
если постоянно генерируется только один символ (![]() или
или ![]() ).
Энтропии в диапазоне от 0 до 1 характеризуют степень порядка в
последовательности. Значения вблизи нуля указывают на то, что один символ
доминирует, например,
).
Энтропии в диапазоне от 0 до 1 характеризуют степень порядка в
последовательности. Значения вблизи нуля указывают на то, что один символ
доминирует, например,
![]() для
для ![]() и
и ![]() . Если же
вероятности почти одинаковы, то значение
. Если же
вероятности почти одинаковы, то значение ![]() близко к 1, например,
близко к 1, например,
![]() для
для ![]() и
и ![]() .
.
Однако, рассматриваемое определение энтропии дает не так уж много полезной
информации. Например, принципиально различные процессы могут иметь одно и то
же значение энтропии. Рассмотрим две последовательности:
и
Если в обоих случаях
Данный недостаток можно устранить, если вычислять блочные энтропии
(или энтропии высокого порядка). Рассмотрим вначале вероятности встретить
различные блоки из 2-х символов: ``00'', ``01'', ``10'', ``11''. Если мы будем
анализировать вероятности данных блоков для последовательностей ![]() и
и
![]() , то получатся различные величины. Можно ввести более общую
характеристику -
, то получатся различные величины. Можно ввести более общую
характеристику - ![]() -блочную энтропию:
-блочную энтропию:
которая определяет среднее количество информации, содержащееся в блоке из
Если энтропии отдельных символов не позволяют получать много информации об
особенностях анализируемых последовательностей, то блочные
энтропии
![]() служат более информативными
характеристиками структуры последовательностей символов. В частных случаях
может наблюдаться характерное поведение для блочных энтропий:
служат более информативными
характеристиками структуры последовательностей символов. В частных случаях
может наблюдаться характерное поведение для блочных энтропий:
- Для последовательности Бернулли (последовательности, в которой любые блоки
из
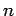 символов имеют равные вероятности
символов имеют равные вероятности
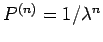 ):
):
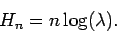
- Для марковских процессов порядка
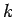 наблюдается линейный рост энтропий при
наблюдается линейный рост энтропий при
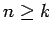 :
:
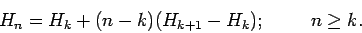
- Для периодических последовательностей с периодом
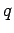 достаточно знать только
достаточно знать только
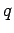 символов, поскольку остальные не несут новой информации. Вследствие
этого
символов, поскольку остальные не несут новой информации. Вследствие
этого
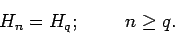
Символьные последовательности, несущие какую-либо полезную информацию, должны
находиться между случаем полной неупорядоченности и периодическими
последовательностями. Для них приращения ![]() уменьшаются при
возрастании
уменьшаются при
возрастании ![]() , что является следствием эффектов ``длительной
памяти''. Чтобы охарактеризовать приращения блочных энтропий, рассматривают
так называемые разностные блочные энтропии (называемые также динамическими
энтропиями):
, что является следствием эффектов ``длительной
памяти''. Чтобы охарактеризовать приращения блочных энтропий, рассматривают
так называемые разностные блочные энтропии (называемые также динамическими
энтропиями):
Их можно интерпретировать как среднюю неопределенность о символе, если известны
называется энтропией источника.
При практических вычислениях блочных энтропий и энтропии источника нужно
обращать внимание на возможность достоверной оценки вероятностей различных
блоков. На практике их определяют как относительную частоту появления того
или иного блока:
где
Энтропию источника иногда определяют другим способом (без расчета
блочных энтропий). В качестве примера рассмотрим определение сложности
Лемпеля-Зива. Идея предложенного ими алгоритма состоит в следующем.
Последовательность символов разбивается на фрагменты, и метками отмечаются
фрагменты, которые ранее еще не были идентифицированы. Например, пусть есть
последовательность ![]() и мы определяем различные фрагменты:
и мы определяем различные фрагменты:
![]() . Число полученных таким способом фрагментов
. Число полученных таким способом фрагментов
![]() может служить мерой сложности. Естественно, что в общем случае
может служить мерой сложности. Естественно, что в общем случае ![]() будет увеличиваться с ростом числа символов
будет увеличиваться с ростом числа символов ![]() последовательности. Для
случайных бинарных кодов (
последовательности. Для
случайных бинарных кодов (![]() ) с ростом
) с ростом ![]() наблюдается
следующее поведение для числа фрагментов:
наблюдается
следующее поведение для числа фрагментов:
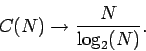
Для не совсем случайных последовательностей
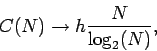
где
Возможность разбить последовательность символов на участки по определенным правилам имеет важное значение в задачах сжатия данных. Одним из потенциальных приложений задач об исследовании мер сложности является создание алгоритмов оптимального архивирования данных. В частности, подход Лемпеля-Зива реализован в известной программе ``gzip''.