Пуанкаре предложил ставший классическим метод анализа динамических систем.
Этот метод позволяет заменить потоковую систему n-го порядка на отображение (n-1)-го порядка с дискретным временем, называемое отображением Пуанкаре.
Определение отображения Пуанкаре гарантирует, что его предельные множества соответствуют предельным множествам указанной потоковой системы. Полезность отображений Пуанкаре состоит в понижении порядка системы и в том факте, что они служат мостом между системами с непрерывным и дискретным временем.
Определение отображения Пуанкаре различно для автономных и неавтономных систем. Рассмотрим оба этих случая отдельно.
Напомним, что периодическая во времени неавтономная система n-го порядка с минимальным периодом T может быть преобразована в автономную систему (n+1)-го порядка в цилиндрическом фазовом пространстве с помощью преобразования

Рассмотрим n-мерную гиперплоскость
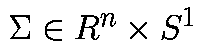
определенную как
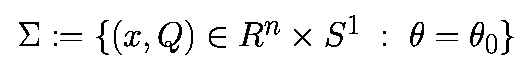
Каждые T секунд траектория системы пересекает гиперплоскость "сигма" (см. рис.1)
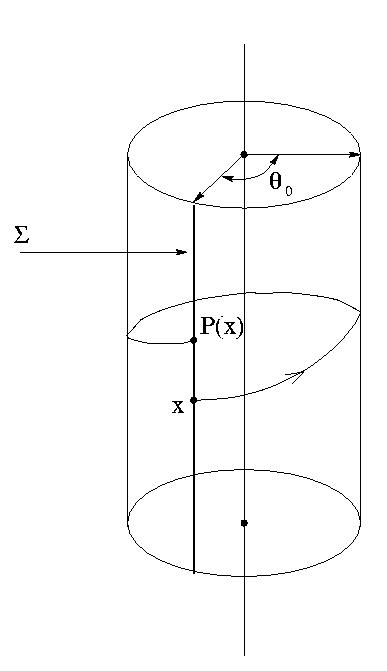
Рис.1 Отображение Пуанкаре для неавтономной системы 1-го порядка.
Получаемое отображение
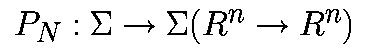
определяется как:
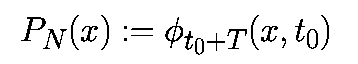
PN называется отображением Пуанкаре неавтономной системы.
Индекс N указывает на неавтономную систему, и служит для отличия этого отображения от отображений Пуанкаре, которые используются в автономных системах. Отметим, что для фиксированного t, фt есть диффеоморфизм и, следовательно, Pn можно представлять себе двумя способами:
1. PN показывает, какое значение примет x через T секунд.
Это называется отображением сдвига на время Т.
2. Орбита
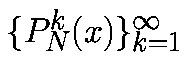
моделирует отдельную траекторию с интервалом в T секунд, т.е.
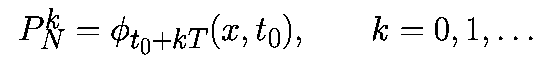
Это похоже на стробоскопическое высвечивание точек траектории с периодом T.
Рассмотрим автономную систему n-го порядка с предельным циклом Г, показанном на рис.2.
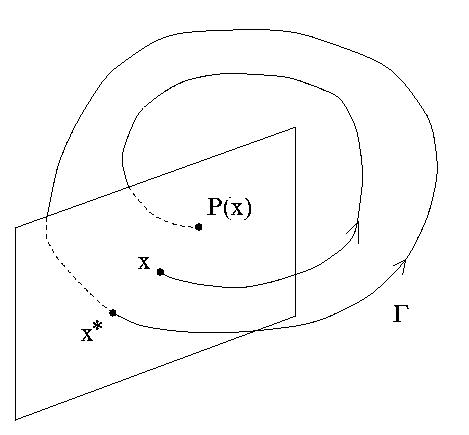
Рис.2 Отображение Пуанкаре для автономной системы 3-го порядка.
Пусть x* - точка на предельном цикле, и пусть "сигма" - n-мерная гиперплоскость, трансверсальная к Г в точке x*. Траектория, выходящая из x*, через T секунд снова попадет в точку x* на гиперплоскости "сигма" (T - минимальный период предельного цикла). В силу непрерывности потока фt по начальным условиям, траектории, начинающиеся на "сигма" в достаточно малой окрестности точки x*, будут, примерно, через T секунд пересекать "сигма" вблизи точки x*.
Следовательно, фt и "сигма" определяют отображение PA в некоторой окрестности U точки x* в другую окрестность U точки x*.
PA есть отображение Пуанкаре автономной системы.
Замечания:
1. PA определено локально, то есть, в окрестности x*. В отличие от неавтономного случая, здесь нет гарантии, что траектория, вышедшая из точки на "сигма" снова пересечет "сигма".
2. Для эвклидова фазового пространства, точка PA(x) не является первой точкой, в которой поток фt пересечет "сигма"; фt(x) должен пройти через "сигма" по крайней мере еще один раз, прежде чем возвратиться в U. В этом, также, заключается отличие от цилиндрического фазового пространства на рис.1.
3. PA является диффеоморфизмом и, следовательно, обратимо и дифференцируемо.
Только что приведенное определение отображения Пуанкаре является стандартным определением, взятым из теории динамических систем, но оно редко используется при численном моделировании, поскольку предполагает предварительное знание положения предельного цикла.
На практике выбирают (n-1)-мерную гиперплоскость "сигма", которая разделяет RN на две области:
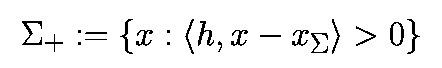
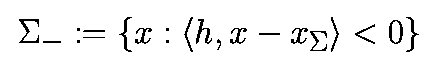
где h есть вектор, нормальный к "сигма" и x - некоторая точка, лежащая на гиперплоскости, и
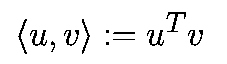
- скалярное произведение. Если "сигма" выбрана правильно, то наблюдаемая траектория будет повторно пересекать "сигма", переходя из "сигма-" в "сигма+", и затем обратно и т.д., как показано на рис.3.
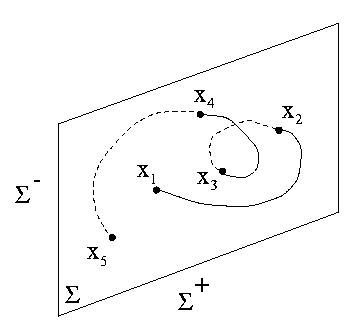
Рис.3 Типичная траектория, пересекающая секущую плоскость "сигма". Последовательность {x1, x3, x5, ...} является орбитой одностороннего отображения Пуанкаре P+, а {x2, x4, ...} - орбитой P-. Полная последовательность {x1, x2, ...} является орбитой двустороннего отображения Пуанкаре P+-.
Для заданной гиперплоскости "сигма" могут быть определены три различных отображения Пуанкаре:
P+: P+(x) - это точка, в которой фt(x) первый раз пересекает "сигма" в положительном направлении, т.е.
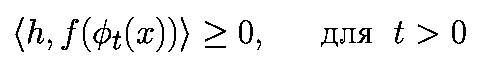
P-: P-(x) - это точка, в которой фt(x) первый раз пересекает "сигма" в отрицательном направлении, т.е.
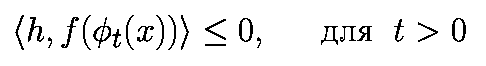
P+-: P+-(x) - это первая точка, в которой фt(x) пересекает "сигма" в каком-либо направлении при t>0.
P+ и P- называются односторонними отображениями Пуанкаре, в то время как P+- называется двусторонним отображением Пуанкаре. Отметим, что точка, в которой траектория касается гиперплоскости, т.е. x на "сигма", для которой
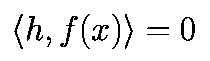
удовлетворяет критериям каждого из трех отображений.
Для любого из этих отображений нет гарантии, что оно хорошо определено, поскольку фt(x) может никогда не пересечь "сигма" для t>0. Для системы с эвклидовым фазовым пространством, которая не стремится к состоянию равновесия, всегда можно выбрать гиперплоскость, для которой все три отображения хорошо определены. Это утверждение не верно для системы с неэвклидовым фазовым пространством.
В качестве примера рассмотрим отображение Пуанкаре неавтономной системы. Поскольку траектория всегда пересекает "сигма" в одном и том же направлении, одно из односторонних отображений Пуанкаре оказывается неопределено; будет это P+ или P-, зависит от выбора вектора нормали h.
Если одно из отображений хорошо определено, непрерывность, и, следовательно, дифференцируемость еще не гарантированы; однако, если f трансверсально к "сигма" в точке x и в точке P(x), тогда отображение локально дифференцируемо.
Отображение PA связано с тремя определенными выше отображениями следующим образом.
В эвклидовом фазовом пространстве траектория, выходящая из фиксированной точки x, может пересекать "сигма" более чем один раз, прежде чем возвращается в x*.
Пусть будет k пересечений, включая окончательное возвращение в x*, и предположим, что все пересечения являются трансверсальными.
Тогда PA эквивалентен k-раз примененному отображению P+, то есть PA(x)=P+-k(x).
Заметим, что в эвклидовом пространстве k всегда будет четным, и следовательно PA будет эквивалентно k/2-применениям P+ или P-; будет ли применено P+ или P-, зависит от того, направленно f(x*) в "сигма+" или "сигма-".
Рассмотрим взаимосвязь между предельными множествами отображений Пуанкаре и предельными множествами исходных потоков. Кроме специально оговоренных случаев, обсуждение будет касаться устойчивых предельных множеств систем в эвклидовом фазовом пространстве.
Не существует предельного множества отображения Пуанкаре, соответствующего точке равновесия.
Обсудим отдельно автономный и неавтономный случай, но вначале приведем два определения.
x* - есть неподвижная точка отображения P, если x*=P(x*).
Множество {x*1,...,x*K} - есть замкнутая орбита периода K отображения P, если x*k+1= Pk, где k=1,...,K-1 и x*1=P*K.
Решение периода один системы с непрерывным временем соответствует неподвижной точке x* отображения Пуанкаре PN. Субгармоника K-го порядка соответствует замкнутой орбите периода K{x*1,...,x*k} отображения Пуанкаре.
Замечание: Отображение Пуанкаре "замораживает" любую периодическую компоненту решения, которая имеет период, соизмеримый с периодом вынуждающей силы. Такое действие аналогично стробоскопическому высвечиванию изображающей точки.
PA: предельный цикл потока фt соответствует неподвижной точке x* отображения PA.
Замкнутая орбита периода K отображения PA указывает на субгармоническое решение исходного потока. Напомним, что надо быть осторожным при использовании термина "субгармоническое решение" в автономных системах. В частности, если минимальный период цикла Г есть T, то минимальный период субгармоники K-го порядка будет близок, но обычно не равен KT, поскольку, в отличие от отображения Пуанкаре для неавтономных систем PA, определяется из условия пересечения, а не из временных условий. Таким образом, время возврата в x* равно T, но время возврата для точки вблизи x* близко, но обычно не равно T.
P+, P- и P+-: Для этих отображений классификация предельных циклов не является однозначной, поскольку предельное множество отображения Пуанкаре зависит от положения секущей гиперплоскости "сигма". В частности, для заданного предельного цикла исходного потока, различный выбор "сигма" может приводить к возникновению замкнутых орбит различных порядков (рис.4).
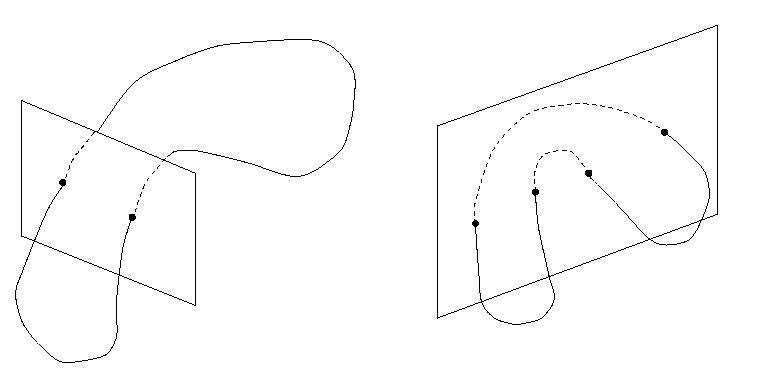
Рис.4 Предельные множества односторонних и двусторонних отображений Пуанкаре зависят от выбора секущей плоскости "сигма".
Наиболее общее утверждение, которое может быть сделано, состоит в том, что замкнутая орбита одного из этих отображений Пуанкаре соответствует предельному циклу исходного потока.
В эвклидовом фазовом пространстве, если предельный цикл пресекает "сигма" трансверсально при каждом пересечении, то порядок соответствующей замкнутой орбиты отображения P+ равен порядку соответствующей замкнутой орбиты отображения P- и равен половине порядка соответствующей замкнутой орбиты отображения P+-.
Почти любое возмущение гиперповерхности "сигма" приводит к исчезновению нетрансверсальных пересечений (касаний). Обобщая, можно сказать, что все замкнутые орбиты отображения P+- имеют четный порядок.
Если быть внимательным, то можно с помощью этих отображений определить субгармонику. Рассмотрим замкнутую орбиту периода m (с трансверсальными пересечениями), которая соответствует предельному циклу Г с периодом T. Если вблизи имеется замкнутая орбита периода mk, то она представляет собой субгармонику K-го порядка по отношению к Г, и период соответствующего ему исходного предельного цикла равен kT.
Ключевым словом здесь является слово "вблизи", поскольку, если две орбиты не расположены близко друг от друга, они могут быть порождены совершенно невзаимосвязанными предельными циклами.