Ляпуновские показатели являются обобщением собственных значений в состоянии равновесия и мультипликаторов. Они могут быть использованы для определения устойчивости квазипериодического и хаотического поведения так же как и для определения устойчивости состояний равновесия и периодических решений.
Возьмем любое начальное состояние
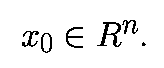
Пусть m1(t),...,mn(t) - собственные значения Фt(x0). Ляпуновские показатели для начального условия x0 есть
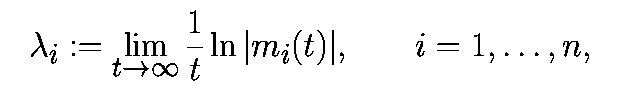
если предел существует.
Возьмем любое начальное состояние x0 и пусть
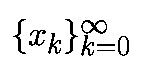
- соответствующая орбита p-мерной системы p с дискретным временем. Пусть m1(k),...,mp(k) - собственные значения матрицы DPk(x0). Ляпуновские числа для начального условия x0 есть
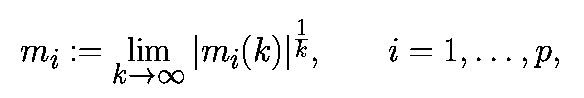
если предел существует.
Чтобы получить представление о Ляпуновских показателях, найдем Ляпуновские показатели состояния равновесия xeq. Общепринято использовать букву лямбда для обозначения собственных значений в состоянии равновесия так же как и для обозначения Ляпуновских показателей. Чтобы различать их между собой мы используем для обозначения собственных значений в состоянии равновесия символ "лямбда с крышечкой".
Пусть
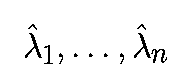
- собственные значения матрицы Df(xeq). Можно показать, что
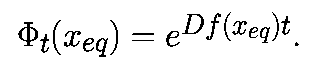
Отсюда следует, что
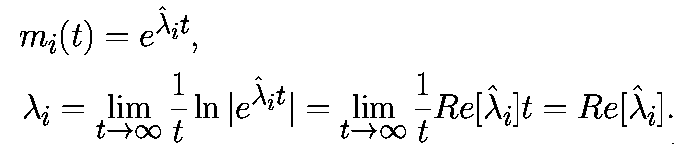
Следовательно, Ляпуновские показатели равны действительным частям собственных значений в состоянии равновесия. Они определяют скорость сжатия (если лямбда отрицательна) или растяжения (если она положительна) вблизи состояния равновесия. Более того, собственные вектора матрицы Df(xeq) определяют подпространство, в котором имеет место растяжение или сжатие.
Согласно определению, Ляпуновские показатели зависят от начального условия. Предположим, что x0 отлично от xeq, но Фt(x0) > xeq при t стремящимся к бесконечности и x0 лежит в бассейне притяжения состояния равновесия. Поскольку Ляпуновские показатели определяются через предел t стремится к бесконечности, любым переходным процессом можно пренебречь и, следовательно, Ляпуновские показатели в состоянии равновесия xeq и точке x0 будут одинаковыми. Вообще говоря, каждая точка в бассейне притяжения аттрактора имеет те же Ляпуновские показатели, что и аттрактор, и удобно говорить о Ляпуновских показателях аттрактора.
Рассмотрим неподвижную точку x* p-мерного отображения P. Пусть
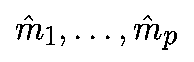
- мультипликаторы отображения P в точке x*, то есть, mi есть собственные значения матрицы DP(x*). Поскольку DPk(x*)=DP(x*)k, собственные значения DPk(x*) есть
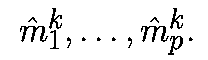
Ляпуновские числа неподвижной точки будут:
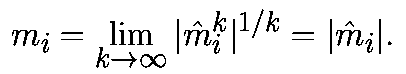
Следовательно, Ляпуновские числа равны абсолютным величинам мультипликаторов в неподвижной точке. Они определяют величину сжатия (если mi < 1) или растяжения (если mi > 1) за одну итерацию в окресности x*. Более того, собственные вектора матрицы DP(x*) определяют подпространство, в котором имеет место растяжение или сжатие.
Предположим, что P - отображение Пуанкаре. Поучительно определить
Ляпуновские показатели исходного периодического решения Г, соответствующего
x*. Пусть T - период Г, и пусть
m1,...,mn - собственные значения матрицы
ФT(x*). В силу периодичности,
ФkT(x*)=ФT(x*)k.
Ляпуновские показатели периодического решения Г есть
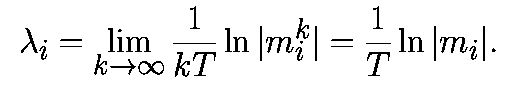
Из этого равенства для mi получаем:
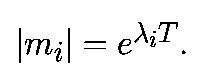
Поскольку |mi| определяет величину сжатия или растяжения за время T, Ляпуновские показатели выражают среднюю скорость сжатия или растяжения в окресности периодического решения. Подпространство, в котором происходит растяжение или сжатие, определяется собственными векторами матрицы ФT(x*).
В автономном случае, одно из собственных значений ФT(x*) всегда равно единице (mn=1 по нашей схеме индексации) и, слежовательно, один Ляпуновский показатель предельного цикла всегда равен нулю.
Как показывают предыдущие примеры, лямюда - есть средняя скорость сжатия (если лямбда отрицательна) или растяжения (если лямбда положительна) в особом подпространстве в окресности отдельного предельного множества.
Что означает выражение "особое подпространство"? Упорядочим лямбда так, что
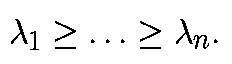
Тогда, в линеаризованной системе имеется n линейных подпространств
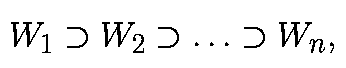
для которых
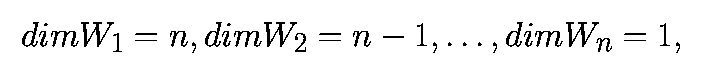
так, что почти все возмущения в Wi в среднем эволюционируют как
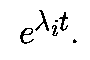
В качестве примера рассмотрим систему третьего порядка в состоянии
равновесия xeq. Предположим, что линеаризованная в xeq
система имеет действительные собственные значения
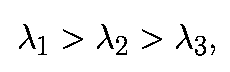
и соответветствующие собственные вектора
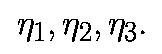
Заметим, что поскольку, собственные значения являются действительными, они равны Ляпуновским показателям. Решение линеаризованной системы записывается в виде:
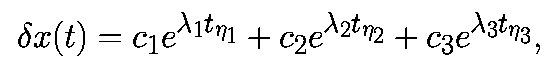
, где
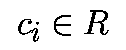
зависят от начального условия.
Для этой системы
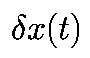
возрастает как
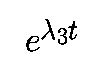
только в том случае, если c1=c2=0; следовательно, W3 есть линия, определяемая вектором
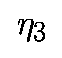
(Как говорят, натянутая на вектор.) Если c1=0, но c2 не равно 0, то
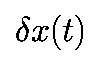
имеет две компоненты
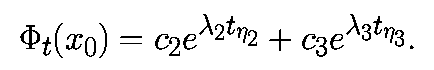
Поскольку
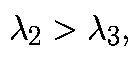
то член
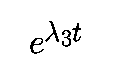
становится пренебрежимо малым на конечном времени, при t стремящимся к бесконечности, возмущение эволюционирует как
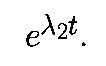
Следовательно, W2 - это плоскость, натянутая на вектора
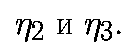
Аналогично,
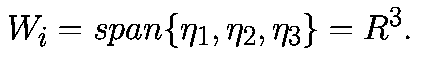
То есть W1 - подпространство, натянутое на вектора
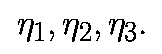
Ляпуновскими показателями удобно пользоваться для характеристики установившихсясостояний. Для аттрактора, сжатие должно преобладать над растяжением, так, что
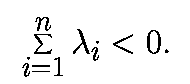
Нехаотические (простые) аттракторы классифицируются следующим образом.
Для асимптотически устойчивого состояния равновесия
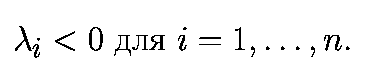
Для асимптотически устойчивого предельного цикла
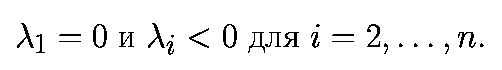
Для асимптотически устойчивого двумерного тора
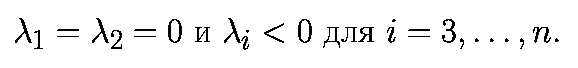
Для асимптотически устойчивого K-мерного тора
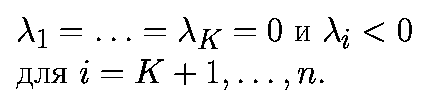
Замечания:
1. Нехаотические аттракторы не имеют положительных Ляпуновских показателей.
2. В случаях общего положения, число нулевых Ляпуновских показателей
нехаотического притягивающего множества определяет топологическую
размерность аттрактора: состояние равновесия характеризуется размерностью,
равной нулю, предельный цикл - размерностью 1, двумерный тор - размерностью
2 и K-мерный тор - размерностью K.
3. Нехаотическое предельное множество является гиперболическим, если его
размерность равна числу нулевых Ляпуновских показателей.
Одной из черт, присущих хаосу, является чувствительность к начальным условиям. Она так же свойственна потокам, в которых присутствует растяжение. Поскольку положительный Ляпуновский показатель указывает на растяжение, то отличительной чертой странных аттракторов, по сравнению с нехаотическими аттракторами, является существование положителього Ляпуновского показателя.
Из тех фактов, что по крайней мере один Ляпуновский показатель хаотической системы должен быть положительным, что один Ляпуновский показатель любого предельного множества кроме состояния равновесия должен быть равен нулю, и, что сумма Ляпуновских показателей аттрактора должна быть отрицательной, следует, что странный аттрактор должен иметь по крайней мере три Ляпуновских показателя. Следовательно, хаос не может возникать в автономных потоковых системах первого и второго порядков, а так же в неавтономных потоковых системах первого порядка.
В трехмерном случае единственная возможность - это (+,0,-), то есть
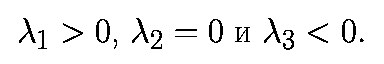
Поскольку сжатие должно преобладать над растяжением, еще одним условием устойчивости трехмерного хаоса будет неравенство
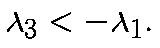
В системах четвертого порядка имеются три возможности:
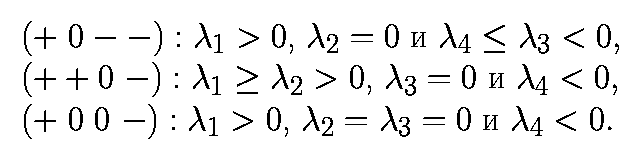
Второй случай Ресслер (1979) назвал гипер-хаосом, третий случай соответствует хаотическому двупериодическому тору. Насколько известно, этот случай никем не наблюдался.
Ляпуновские показатели различных типов предельных множеств даны в
нижеприведенной таблице.
| Состояние равновесия | Притягивающее множество потока | Притягивающее множество отображения пуанкаре | Ляпуновские числа | Размерность |
| Устойчивая точка | Точка | - | 0 > Л1 >= . . . >= Лn | 0 |
| Периодическое движение | Предельный цикл | Одна и более точек | Л1=0 0 > Л2 >= . . . >= Лn |
1 |
| Удвоенный период | Тор | Одна и более замкнутых кривых | Л1=Л2=0 0 > Л3 >= . . . >= Лn |
2 |
| Период порядка K | K-мерный тор | Один и более (K-1)-мерных торов | Л1 = . . . = ЛK=0 0 > ЛK+1 >= . . . >= Лn |
K |
| Хаотическое движение | Канторово множество | Канторово множество | Л1 > 0 Л1 + . . . + Лn < 0 |
не целое |