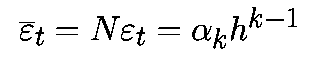Вычисление траекторий представляет собой наиболее важную задачу при
моделировании динамических систем с непрерывным временем. Цель алгоритма
интегрирования заключается в аппроксимации поведения системы с непрерывным
временем с помощью цифрового (по своей сути) компьютера.
Поскольку
вычислительные процессы в компьютере по своей природе дискретны во времени,
алгоритм интегрирования моделирует систему с непрерывным временем
системой с дискретным временем. Фактическая система, полученная при
таком моделировании, не является дифференциальным уравнением. Часто это
сложная система с дискретным временем. Алгоритмы интегрирования
отличаются тем, что отображают одно и то же дифференциальное уравнение в
различные системы с дискретным временем.
Рассмотрим несколько стандартных алгоритмов. Предлагаемые алгоритмы аппроксимируют решение системы с непрерывным временем
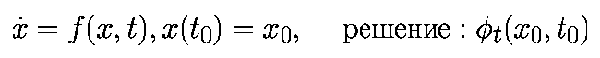
| (1) |
последовательностью точек x0,x1,... в соответствующие моменты времени t0,t1,... Значения точек должны удоволетворять приближенному равенству
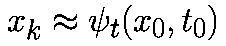
Если специально не оговорено иное, то предполагается, что моменты времени выбираются через равные интервалы с величиной шага h>0, то есть
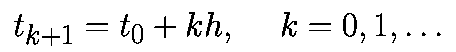
Аппроксимируем производную в момент времени tk соотношением
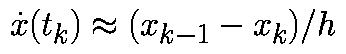
При такой аппроксимации уравнение (1) примет вид:
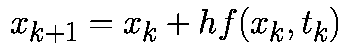
| (2) |
Формула (2) известна как прямой метод Эйлера.
На рис.1(a) показана графическая интерпретация прямого метода Эйлера. На (k+1)-ом шаге векторное поле предполагается (локально) постоянным со значением f(xk,tk).
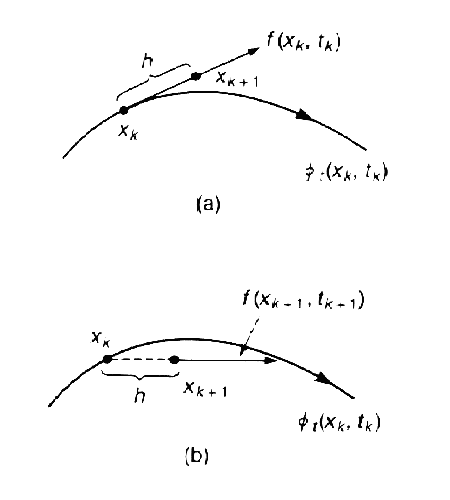
Рис.1 Иллюстрация алгоритмов (а) прямого метода Эйлера, (b) обратного метода Эйлера
Меньшее значение величины шага h в итоге дает точки аппроксимации чаще и, как демонстрирует рис.2, приводит к большей точности интегрирования, что приобретает математический смысл, поскольку (2) стремится к (1) при h->0.
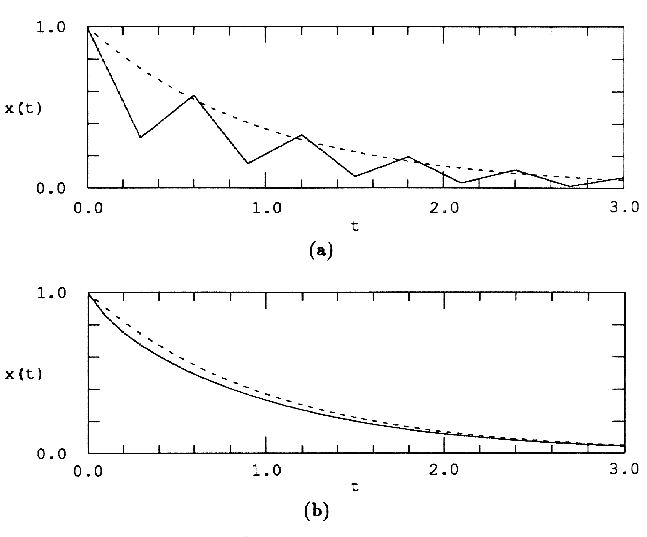
Рис.2 Влияние величины шага. Уравнение dx/dt=-6x+5t-t интегрируется от x=1 прямым методом Эйлера при h=0.3 (а) и при h=0.1 (b). Точное решение показано штриховой линией.
Обратный метод Эйлера подобен прямому, но есть одно отличие в аппроксимации для производной
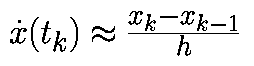 .
.
Такая аппроксимация дает формулу обратного метода Эйлера:
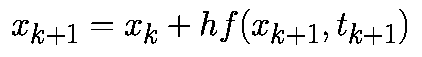
| (3) |
На рис.1(b) показана геометрическая интерпретация обратного метода Эйлера. На (k+1)-ом шаге векторное поле предполагается (локально) постоянным со значением f(xk+1,tk+1).
Обратный метод Эйлера - это пример неявного алгоритма интегрирования , где xk+1 является функцией от самой себя. И напротив, прямой метод Эйлера представляет собой явный алгоритм. В неявных алгоритмах для определения xk+1 требуются дополнительные вычисления, но они по сравнению с аналогичными прямыми алгоритмами более устойчивы и дают более высокую точность вычислений (см. рис.3). Возможно это обусловлено наличием члена xk+1 в правой части формулы, что может рассматриваться как вид обратной связи.
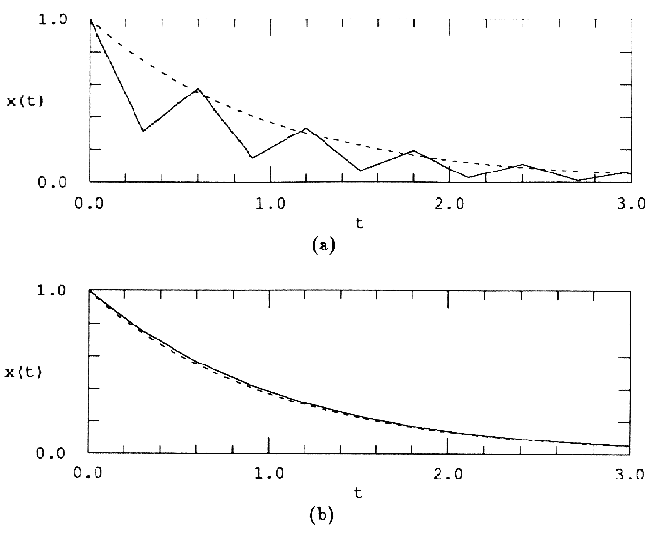
Рис.3 Та же система, что и на рис.2 проинтегрирована от x0=1.0 с h=0.3 (a) прямым методом Эйлера, (b) обратным методом Эйлера. Точное решение показано штриховой линией.
Трапецеидальный алгоритм имеет вид:
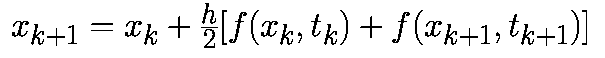
Он относится к явным алгоритмам. Предполагается, что векторное поле (локально) постоянно со значением равным среднему от f(xk,tk) и f(xk+1,tk+1). Алгоритм можно рассматривать как сочетание прямого и обратного алгоритмов Эйлера.
В основу семейства алгоритмов Рунге-Кутта положена идея аппроксимации фt(xk) рядом Тейлора. Рассмотрим алгоритмы второго и четвертого порядков. Термин "k-го порядка" означает, что в аппроксимации используется k членов ряда Тейлора.
Имеется целое семейство уравнений Рунге-Кутта второго порядка. Мы рассмотрим модифицированный алгоритм Эйлера-Коши, заданный соотношением:
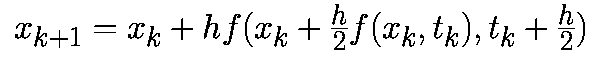
Из этой формулы следует, что модифицированный алгоритм Эйлера-Коши включает два этапа. На первом этапе с помощью прямого метода Эйлера происходит перемещение на пол шага вперед к моменту времени (tk+h/2):
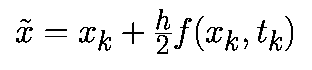
На втором этапе это промежуточное значение используется для аппроксимации векторного поля с помощью итераций Эйлера прямого типа:
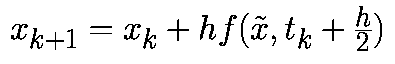
Модифицированный алгоритм Эйлера-Коши использует значение векторного поля в средней точке между xk и xk+1. Он отличается от трапецеидального алгоритма, в котором используется среднее значение векторного поля по xk и xk+1. Его можно рассматривать как явный алгоритм, который, используя промежуточный шаг по времени, включен в неявный алгоритм.
Как и в случае алгоритма второго порядка метод Рунге-Кутта четвертого порядка относится к явным алгоритмам. Он использует промежуточные моменты времени для для вычисления состояния в момент времени tk+1. Следующие формулы определяют алгоритм Рунге-Кутта четвертого порядка:
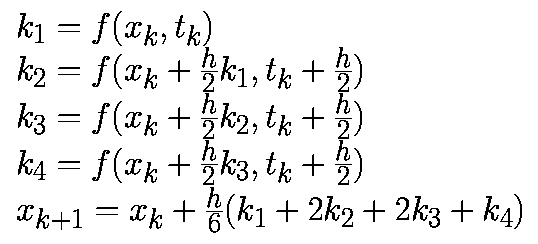
| (4) |
Каждое из четырех Ki является аппроксимирующим значением векторного поля.
K1 - значение векторного поля при xk.
K2 - аппроксимированное значение на полшага позже, в момент времени tk+h/2. В сущности, это прямой метод Эйлера с временным шагом h/2.
K3 - также значение векторного поля в момент tk+h/2, но вычисляется с использованием K2. Это схоже с обратным методом Эйлера с половинным шагом, за исключением того, что вместо неявного разложения (3) используется явная аппроксимация для f в момент времени tk+h/2.
K4 - значение векторного поля в момент tk+1, вычисляется с использованием основного последнего значения K3. Это модифицированный шаг Эйлера-Коши. Наконец, эти четыре значения усредняются, чтобы дать аппроксимацию векторного поля для определения xk+1.
Для определенных выше алгоритмов на каждом шаге требуется только одна начальная точка xk. Такие алгоритмы называются одношаговыми. Одношаговые алгоритмы высокого порядка имеют высокую точность, но они не эффективны, если велики затраты на вычисление f. Например, алгоритм Рунге-Кутта четвертого порядка требует на шаге четыре значения f. Кроме того, на текущем шаге не выполняются оценки функций с целью их использования на последующих шагах.
В отличие от одношаговых алгоритмов, многошаговые алгоритмы повторно используют предыдущую информацию о траектории. В m-шаговом алгоритме для определения xk+1 используют m предыдущих точек xk, xk-1,...,xk-m+1 и значения f в этих точках. Общая формула m-шагового алгоритма имеет вид
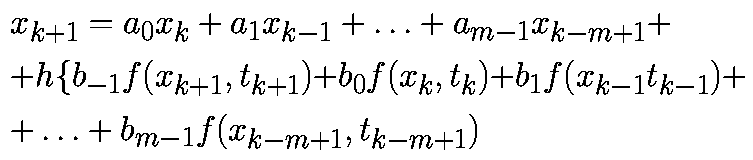
| (5) |
где tk-i - равноотстоящие точки с шагом h.
Задавая различные значения коэффициентов ai и bi, получим различные алгоритмы интегрирования. Отметим, что многошаговый алгоритм будет неявным тогда и только тогда, когда b-1=0, в других случаях он будет явным.
Уравнение (5) очень схоже со стандартной программой интерполяции. Члены ai дают возможность определить xk+1 из предыдущих значений траектории. Члены bi увеличивают точность аппроксимации, используя дополнительную информацию, которая обеспечивается функцией f.
Отметим, что для многошагового алгоритма на шаге требуется только одно новое значение функции (f(xk) - для явных алгоритмов, f(xk+1) - для неявных алгоритмов). Следовательно, на шаге он более эффективен по сравнению с одношаговым алгоритмом.
Однако одношаговый алгоритм (например Рунге-Кутта четвертого порядка) использует дополнительные оценки функций для аппроксимации векторного поля в промежуточных точках и поэтому обычно допускается больший размер шага.
Вообще, заранее невозможно сказать, будет ли более эффективным одношаговый или многошаговый алгоритм. Это зависит от решаемой задачи.
Решение системы с непрерывным временем имеет волновую форму, а результатом алгоритма интегрирования является последовательность точек. Возникает важный вопрос: насколько числа, полученные на компьютере, близки к траектории? Существует два типа ошибок.
Локальная ошибка - это ошибка, вносимая на одном шаге алгоритма интегрирования.
Глобальная ошибка - это общая ошибка, обусловленная повторными применениями формулы интегрирования.
Пользователей интересует глобальная ошибка. К сожалению, из-за сложности вычисления глобальной ошибки, большинство современных работ сосредоточены на оценке локальной ошибки.
Локальная ошибка определяется как ошибка на шаге алгоритма:
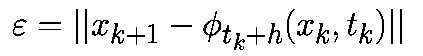
Для m-шаговых алгоритмов предполагается, что предыдущие m точек xk-i при i=0,...m-1 являются точно заданными, т.е.
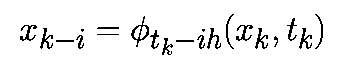
Таким образом локальная ошибка не учитывается при накоплении ошибок от одного шага к последующему. Имеется два типа локальных ошибок: ошибка округления и ошибка усечения.
Ошибка округления - это неизбежная ошибка, которая возникает в результате выполнения арифметических действий на цифровом компьютере. Величина ошибки округления зависит от используемого аппаратного обеспечения и трудно предсказать, как различные алгоритмы будут реагировать при их выполнении на различных типах машин. Однако отметим, что ошибка округления зависит от числа и типа арифметических операций на шаге и, следовательно, не зависит от величины шага интегрирования.
Если компьютер выбран, то единственный способ ограничить локальную ошибку округления - это увеличить точность представления чисел с плавующей точкой. Обычно представление с одинарной точностью использует 32 бита и является точным в пределах семи десятичных разрядов; большинство представлений с двойной точностью используют 64 бита и являются точными в пределах пятнадцати десятичных разрядов.
Ошибка усечения - это локальная ошибка, которая получилась бы в результате выполнения алгоритма на компьютере с бесконечной точностью.
Другими словами, подразумевается, что эта локальная ошибка возникает помимо ошибки округления. Также важно помнить, что для m-шаговых алгоритмов предыдущие m точек xk,...,xk-m+1 предполагаются точно заданными.
Ошибка усечения берет свое название от алгоритмов, основанных на рядах Тейлора (например, Рунге-Кутта). Эти алгоритмы были бы точными, если бы использовались полные (бесконечные) ряды. Ошибка возникает при усечении ряда до конечного числа членов.
Ошибка усечения зависит только от алгоритма. Она не зависит от используемого компьютера и, следовательно, может быть проанализирована. Для алгоритмов Рунге-Кутта K-го порядка, при подходящих условиях, локальная ошибка усечения представляет собой
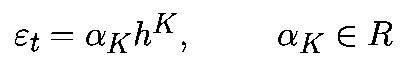
где "альфа" зависит от K, f и xk, но не зависит от h. Для многошагового алгоритма K-го порядка локальная ошибка усечения имеет вид
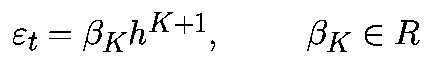
где "бэта" зависит от m, K, f, xk, использует многошаговый алгоритм и не зависит от h.
Рассмотрим глобальное влияние локальных ошибок. Предполагается, что система интегрируется на единичном интервале от t0 до (t0+1) с величиной шага h<<1. Общее число шагов интегрирования составляет N=1/h.
Глобальнае ошибка округления - это простое накопление локальных ошибок округления. Если локальная ошибка составляет "эпсилон", то ошибка округления на единичном интервале будет
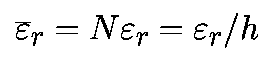
Таким образом, глобальная ошибка округления обратно пропорциональна величине шага. Другими словами, большая величина шага приводит к меньшей глобальной ошибке.
Подобно ошибке округления, локальная ошибка усечения также накапливается с каждым шагом. Для одношаговых алгоритмов K-го порядка локальная ошибка усечения составляет
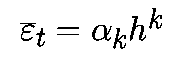
Если пренебречь зависимостью ak от xk, то на единичном интервале времени ошибка усечения будет: