П2. Оценивание основных свойств реализаций

Следующим важным этапом предварительного анализа является оценивание основных свойств реализаций случайных процессов. К основным свойствам относится стационарность, нормальность и наличие периодических составляющих. Предварительная оценка основных характеристик позволяет упростить исследование свойств временных рядов, например, выявление стационарности дает возможность изучать временной ряд классическими методами, которые существенно проще, чем методы анализа нестационарных реализаций. Если установлено, что временной ряд содержит периодические составляющие, то это позволяет избежать ошибок, связанных с неправильной интерпретацией результатов анализа.

1. Проверка стационарности

Способы проверки стационарности могут быть самыми различными -- от визуального контроля временного ряда опытным специалистом до детального статистического оценивания свойств реализаций СП. Во всех случаях предполагается, что временной ряд правильно отражает характер изучаемого процесса. Очевидно, что из всех возможных способов анализа наибольшую ценность представляют формализованные, которые могут быть использованы неспециалистами в области анализа случайных процессов. Эти способы состоят в проверке зависимости (или независимости) параметров реализации от начала отсчета времени. В качестве параметров, как правило, выбирают среднее значение, дисперсию, реже моментные функции более высоких порядков и функцию плотности вероятности. В зависимости от выбранной характеристики говорят о стационарности временного ряда относительно среднего значения или дисперсии и т. д. Отметим, что временной ряд может быть стационарен относительно одного параметра, например, среднего значения, но проявлять нестационарность относительно другого, например, дисперсии.

Общий алгоритм проверки временного ряда $x(i)$ длины $N$ на стационарность следующий:

1. Временной ряд делится на $M$ равных интервалов, причем наблюдения в разных интервалах полагаются независимыми.

2. Вычисляются оценки параметров ряда (среднего значения, дисперсии и т. п.) для каждого интервала. Эти оценки образуют последовательность, или временной ряд оценок параметров $y_i$, $1\le i \le M$, например, ряд средних значений $\mu_i$.

3. Временной ряд оценок проверяется на наличие тренда или других изменений во времени, которые нельзя объяснить только выборочной изменчивостью оценок. Если тренд оценки существует, то ряд рассматривается как нестационарный по этой оценке.

В основе проверки на наличие тренда лежит тот факт, что для стационарной реализации оценки, вычисленные по разным интервалам ряда, являются независимыми случайными величинами. Другими словами, необходимо провести тест на статистическую зависимость между элементами временного ряда оценок $y_i$. Такой тест может быть осуществлен различными способами (в том числе визуальным), которые включают как параметрические, так и непараметрические критерии. Параметрические критерии можно использовать, если известна частотная структура процесса. Как правило, такая информация отсутствует, поэтому применяются непараметрические критерии, например, критерий инверсий, который представляет собой наиболее мощное средство для обнаружения монотонных трендов во временных рядах и проверки гипотезы о статистической независимости наблюдений.

Рассмотрим процедуру построения критерия инверсий для проверки статистической независимости величин $y_i$, $1\le i \le M$. Процедура заключена в подсчете того, сколько раз в последовательности имеют место неравенства $y_k>y_i$ при $k<i$. Каждое такое неравенство называется инверсией. Обозначим через $A$ общее количество инверсий. Формальная процедура подсчета инверсий выглядит следующим образом. Определим для последовательности $y_i$ величины $h_{ki}$:

$$\begin{eqnarray*} h_{ki}=\left\{ \begin{array}{cc} 1,&y_k>y_i, k<i,\\ 0,&y_k\le y_i. \end{array}\right. \end{eqnarray*}$$

Тогда число инверсий вычисляется следующим образом:

$$\begin{eqnarray*} A=\sum_{k=1}^{M-1}A_k,\ \ \ A_k=\sum_{i=k+1}^{M}h_{ki}. \end{eqnarray*}$$

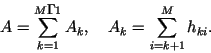
Пример. Рассмотрим последовательность из 8 наблюдений: $y_1=5$, $y_2=3$, $y_3=8$, $y_4=9$, $y_5=4$, $y_6=1$, $y_7=7$, $y_8=5$. В этой последовательности $y_1>y_2$, $y_1>y_5$ и $y_1>y_6$, т.е. $A_1=3$ -- число инверсий для $y_1$. Теперь сравним $y_2$ с последующими за ним наблюдениями. Обнаруживаем, что число инверсий для $y_2$ равно $A_2=1$. Продолжив эту процедуру, найдем, что $A_3=4$, $A_4=4$, $A_5=1$, $A_6=0$ и $A_7=1$, а общее число инверсий равно $A=14$.

Если временной ряд $y_i$ состоит из независимых наблюдений, то число инверсий является случайной величиной, распределенной по нормальному закону со среднем значением и дисперсией, равными соответственно

$$\begin{eqnarray*}\mu_A=\frac{M(M-1)}{4},\ \ \ \sigma^2_A=\frac{M(2M+5)(M-1)}{72}. \end{eqnarray*}$$

Чтобы осуществить проверку гипотезы о статистической независимости значений ряда $y_i$ необходимо задать уровень значимости $\alpha$, который определяет границы области принятия гипотезы $A_{1-\alpha/2}$ и $A_{\alpha/2}$. Если значение $A$ лежит вне указанных границ, то гипотеза о статистической независимости элементов временного ряда и, соответственно, о стационарности ряда должна быть отвергнута. Границы области принятия гипотезы можно найти численным решением следующих уравнений:

$$\begin{eqnarray*} P(z_{\alpha/2})=\int_{-\infty}^{z_{\alpha/2}}p(z)dz=1-\alpha/2... ...ft ( \frac {-z^2}{2} \right) , \ \ \ z=\frac{A-\mu_A}{\sigma_A}. \end{eqnarray*}$$

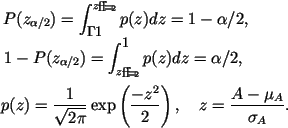
Уровень значимости обычно выбирают равным $\alpha=0.05$, что означает принятие или непринятие гипотезы с доверительной вероятностью 95%.

Для рассмотренной в примере последовательности из 8 наблюдений границы области принятия гипотезы c уровнем значимости $\alpha=0.05$ принимают значения $A_{1-\alpha/2}=6$ и $A_{\alpha/2}=22$. Общее число инверсий ($A=14$) лежит внутри этого интервала и, следовательно, гипотеза о статистической независимости $y_i$ является справедливой.

Более подробно о процедуре проверки статистических гипотез можно узнать из литературы по математической статистике [4,10,11,12,16].

В некоторых случаях независимость моментных функций от начала отсчета времени может быть недостаточным доказательством стационарности, например, если спектр временного ряда сильно нестационарен. В этом случае временной ряд в частотной области разбивается на несколько смежных частотных диапазонов при помощи полосовых фильтров и отдельно проверяется стационарность относительно моментных функций в каждом диапазоне.

2. Проверка периодичности

Периодические и почти периодические составляющие во временном ряде диагностируются по наличию дельта-пиков в спектральной плотности. Однако на практике часто возникают трудности, связанные с конечным частотным разрешением спектра мощности и эффектами конечной длины выборки. Если спектральная плотность содержит острые пики, то они могут принадлежать как периодической составляющей временного ряда, так и узкополосной случайной составляющей. Если рассчитать спектр мощности несколько раз со все более высоким разрешением по частоте, то можно отличить гармонический сигнал от узкополосного шума: для гармонического сигнала ширина спектрального пика уменьшается, а высота растет пропорционально уменьшению ширины пика; для узкополосного шума ширина пика сначала может уменьшаться, но, начиная с некоторых значений спектрального разрешения, не меняется. Для того, чтобы реализовать данную процедуру проверки периодичности, необходимо менять спектральное разрешение в широкой области; это осуществляется путем изменения частоты дискретизации, но не всегда является возможным. Поэтому дополнительно проводится визуальный анализ плотности вероятности и корреляционной функции, которые качественно отличаются для гармонического сигнала и шума. Так, плотность вероятности гармонического сигнала имеет два характерных максимума, а распределение шума является гауссовым; корреляционная функция шумового процесса стремится к нулю при увеличении временного сдвига $\tau$, а для гармонического сигнала эта функция демонстрирует осцилляции.

3. Проверка нормальности

Важность данного этапа обусловлена особым местом нормальной (гауссовой) плотности вероятности среди различных функций распределения: для нахождения параметров математической модели временного ряда с гауссовой плотностью вероятности достаточно оценить лишь среднее значение и дисперсию ряда.

Проверка реализации СП на нормальность осуществляется после того, как выяснено, что процесс стационарный, а также идентифицированы и исключены периодические составляющие.

Наиболее простым способом проверки на нормальность является измерение плотности вероятности значений временного ряда и сравнение ее с теоретическим нормальным распределением. Если длина временного ряда достаточно велика и ошибки измерений малы по сравнению с отклонениями плотности вероятности от нормальной кривой, то несоответствие функции нормальному распределению будет очевидным. Кроме того, можно рассчитать асимметрию и эксцесс, значения которых для гауссова процесса равны соответственно $A=0$, $E=3\sigma^4$. В сомнительных случаях проверку на нормальность можно продолжить, используя критерии согласия, например, критерий $\chi$-квадрат [4,11].