Controlling Spatiotemporal Chaos in One- and Two-Dimensional Coupled Logistic Map Lattices
Vladimir V. Astakhov, Vadim S. Anishchenko,
Galina I. Strelkova,
Alexey V. Shabunin
Laboratory of Nonlinear Dynamics,
Saratov State University, Saratov, Russia
Abstract. A method of control of spatiotemporal chaos in lattices of coupled maps is proposed in this work. Forms of spatiotemporal perturbations of a system parameter are analytically determined for one- and two-dimensional logistic map lattices with different kinds of coupling to stabilize chosen spatiotemporal states previously unstable. The results are illustrated by numerical simulation. Controlled transition from the regime of spatiotemporal chaos to the previously chosen regular spatiotemporal patterns is demonstrated.
INTRODUCTION
Recently, in the frames of the dynamical chaos theory there has appeared a new branch. It is the control of chaos, e.g. transformation of initial chaotic behaviour of the system to the desired regular one by means of small influences on the system. This problem is connected with different fields of science and attracts a growing interest due to its potential applications (1-13).
Now, the possibility of effective control of temporal chaos has been investigated rather well. A number of works devoted to the important problem of controlling spatiotemporal chaos in high-dimensional and distributed systems has also appeared (10-13), which has suggested some methods of controlling chaos in coupled map chains.
In this work we propose a way of spatiotemporal chaos control in coupled map lattices. Forms of spatiotemporal perturbations of a system parameter are analytically determined for one- and two-dimensional coupled logistic map lattices to convert the systems to the chosen regular spatiotemporal states of the lattice. Controlled transitions of the system from the regime of spatiotemporal chaos to the spatio-homogeneous regimes with temporal periods one, two, four and to more complicated regular regimes with different spatial and temporal periods have been demonstrated by numerical simulations.
CONTROL OF SPATIOTEMPORAL CHAOS IN ONE-DIMENSIONAL COUPLED MAP LATTICES
We shall consider the coupled logistic map chains with two types of coupling.
![]()
![]()
with periodic boundary conditions ![]() , where
, where ![]() is
the parameter of nonlinearity,
is
the parameter of nonlinearity, ![]() is the coefficient of coupling
and
is the coefficient of coupling
and ![]() is a value of the dynamical variable in the point with discrete
coordinate i and in discrete time moment n (
is a value of the dynamical variable in the point with discrete
coordinate i and in discrete time moment n ( ![]() where N is the number of elements in the chain). With varying parameters
where N is the number of elements in the chain). With varying parameters
![]() and
and ![]() , in the systems (1) and (2) there exists complex
spatiotemporal
dynamics. For example, the formation of domain
structures, different spatio-periodic regimes as well as the regime of
spatial intermittency of competitive structures can occur in system (1).
(14-17). As the parameter
, in the systems (1) and (2) there exists complex
spatiotemporal
dynamics. For example, the formation of domain
structures, different spatio-periodic regimes as well as the regime of
spatial intermittency of competitive structures can occur in system (1).
(14-17). As the parameter ![]() is further
increased, the system transits to the regime of developed spatiotemporal
chaos. In the chain with linear coupling (2) before the critical parameters
values the zigzag unstability prevails. Then, the stable
spatio-periodic regime with wavelength
is further
increased, the system transits to the regime of developed spatiotemporal
chaos. In the chain with linear coupling (2) before the critical parameters
values the zigzag unstability prevails. Then, the stable
spatio-periodic regime with wavelength ![]() and temporal period
T=2 is formed on the basis of the zigzag unstability. While
and temporal period
T=2 is formed on the basis of the zigzag unstability. While
![]() is increased, it is changed
by quasi-periodic
motion, after which the transition to the spatiotemporal chaos takes place.
On the basis of zigzag patterns appearance of defects is also possible
as well as
Brownian motion of the defects and the defect turbulence (14-17).
A variety of different unstable regular spatiotemporal states co-exists
on the chaotic attractor of these systems. There is an important
question,
how to stabilize a chaotic trajectory near these unstable
structures by applying the perturbations on a system parameter.
is increased, it is changed
by quasi-periodic
motion, after which the transition to the spatiotemporal chaos takes place.
On the basis of zigzag patterns appearance of defects is also possible
as well as
Brownian motion of the defects and the defect turbulence (14-17).
A variety of different unstable regular spatiotemporal states co-exists
on the chaotic attractor of these systems. There is an important
question,
how to stabilize a chaotic trajectory near these unstable
structures by applying the perturbations on a system parameter.
Suppose, that unstable spatio-homogeneous states with temporal period T=s
and spatio-periodic structures with wavelength ![]() and temporal period
T=2,
and temporal period
T=2, ![]() and T=2,
and T=2, ![]() and T=4 co-exist in the regime
of chaos.
Consider the simplest case. It is the spatio-homogeneous regime with some
temporal period T=s. Suppose, the element of the chain (1) with
coordinate i
enters a small neighbourhood of the fixed-point
and T=4 co-exist in the regime
of chaos.
Consider the simplest case. It is the spatio-homogeneous regime with some
temporal period T=s. Suppose, the element of the chain (1) with
coordinate i
enters a small neighbourhood of the fixed-point ![]() of the periodic
orbit with period s. Then we present the dynamical variable in the
form:
of the periodic
orbit with period s. Then we present the dynamical variable in the
form:
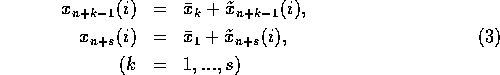
(where ![]() is a small perturbation of the dynamical variable
near the fixed-point
is a small perturbation of the dynamical variable
near the fixed-point ![]() ). We shall consider the parameter of
nonlinearity
). We shall consider the parameter of
nonlinearity ![]() as available for control. Write it in the
form:
as available for control. Write it in the
form:
![]()
(where ![]() is a small perturbation of the parameter
near its nominal value
is a small perturbation of the parameter
near its nominal value ![]() ).
).
Rewrite the system (1), taking into account (3) and (4), as follows:
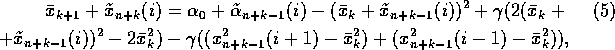
where k=1,...,s.
Suppose, the values of the neighbouring elements with
coordinates i-1 and i+1 differ from the value of the fixed point ![]() by such a magnitude, that the last term in the equation (5) can be comparable
with
by such a magnitude, that the last term in the equation (5) can be comparable
with ![]() . Then, we write the equations for the fixed
point and for the evolution of the dynamical variable perturbation of the
i-th element:
. Then, we write the equations for the fixed
point and for the evolution of the dynamical variable perturbation of the
i-th element:
![]()
![]()
where k=1,...,s.
Choose the parameter perturbations of the i-th element depending on its variable and on the variables of the neigbouring elements as follows:
![]()
Substituting (8) into (7), we obtain coefficients ![]() and
and ![]() at which
the perturbations of the dynamical variable of the i-th
element decrease in time. The form of the parameter perturbation of the
system (1) to convert the system (1) from the regime of spatiotemporal chaos
to the spatio-homogeneous regime with temporal period T=s is as follows:
at which
the perturbations of the dynamical variable of the i-th
element decrease in time. The form of the parameter perturbation of the
system (1) to convert the system (1) from the regime of spatiotemporal chaos
to the spatio-homogeneous regime with temporal period T=s is as follows:
![]()
where k=1,...,s.
To test the obtained results, numerical simulation has been carried out with the
coupled logistic map chain (1).
Let our task be to convert chaotic behaviour to the spatio-homogeneous one
with
T=1. At first, we determine from (6) the value of the fixed point
![]() . Then, having set the values of the parameters
. Then, having set the values of the parameters ![]() and
and ![]() , which correspond to the regime of spatiotemporal chaos,
we wait for the moment in the
evolution of the system when the value of one of elements falls within the
, which correspond to the regime of spatiotemporal chaos,
we wait for the moment in the
evolution of the system when the value of one of elements falls within the
![]() -neighbourhood of the
-neighbourhood of the ![]() . After that, the magnitude
. After that, the magnitude
![]() is evaluated. If it is less than the given
is evaluated. If it is less than the given ![]() , the
parameter perturbation in the form (9) is introduced to influence
this element.
When other elements enter the given neighbourhood, the perturbations
begin to act on their parameters, if the mentioned above condition is
satisfied. Gradual transition of the elements to the chosen state is
observed.
At first, there appear small randomly distributed spatio-homogeneous patterns.
Then, they gradually expand and as the result occupy the whole
chain and a stationary spatio-homogeneous regime is observed
in the system. The process of the control is consistently
illustrated in the fig. 1a. The parameter perturbations having
been turned off, the
system naturally returns to the regime of spatiotemporal chaos.
, the
parameter perturbation in the form (9) is introduced to influence
this element.
When other elements enter the given neighbourhood, the perturbations
begin to act on their parameters, if the mentioned above condition is
satisfied. Gradual transition of the elements to the chosen state is
observed.
At first, there appear small randomly distributed spatio-homogeneous patterns.
Then, they gradually expand and as the result occupy the whole
chain and a stationary spatio-homogeneous regime is observed
in the system. The process of the control is consistently
illustrated in the fig. 1a. The parameter perturbations having
been turned off, the
system naturally returns to the regime of spatiotemporal chaos.
Transformation of chaotic behaviour into a spatio-homogeneous one with
larger temporal period is performed in the similar way. In this case the
form of the parameter perturbation gets complicated as seen from
the expression (9). Thus, to transit to the regime with temporal period two
it is necessary to use two kinds of perturbations. One of them acts when the
system elements enter the neighbourhood of the point ![]() , while
the other perturbation
acts at the next iteration when they enter the neighbourhood of the point
, while
the other perturbation
acts at the next iteration when they enter the neighbourhood of the point
![]() . For the regime with temporal period four, there are four similar
expressions of the perturbations, every of which influences the system parameter
at the determined time moment and so on. The transition of the system from
the regime of
spatiotemporal chaos to the spatio-homogeneous regime with temporal periods
T=2 and T=4 is illustrated in fig. 1b,c.
. For the regime with temporal period four, there are four similar
expressions of the perturbations, every of which influences the system parameter
at the determined time moment and so on. The transition of the system from
the regime of
spatiotemporal chaos to the spatio-homogeneous regime with temporal periods
T=2 and T=4 is illustrated in fig. 1b,c.
It should be mentioned, that both in our investigations and in the work (13), the small patterns of unhomogeneous behaviour remained uncontrollable when the system has been converted to spatio-homogeneous regimes with temporal periods larger than one. To eliminate these dislocations we have applied a small random influence on them. As the result the whole chain has converted to the regimes of spatio-homogeneous motions.
The more complicated situations are controlled
transitions of the chain to spatio-periodic structures with
![]() and T=2,
and T=2, ![]() and T=2, and
and T=2, and ![]() and T=4.
In this case our approach is as follows. We decompose all elements of the
lattice on
and T=4.
In this case our approach is as follows. We decompose all elements of the
lattice on ![]() groups.
The elements
of every such group, located at the distance
groups.
The elements
of every such group, located at the distance ![]() (p=1,2,...)
from each other, have equal values of the dynamical variable
(p=1,2,...)
from each other, have equal values of the dynamical variable
![]() .
Having written the equation (1) for every group of the elements we obtain
the system of equations:
.
Having written the equation (1) for every group of the elements we obtain
the system of equations:
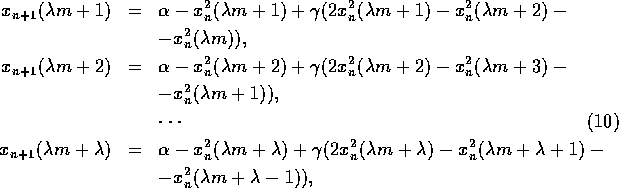
![]() .
Then, using the system (10) and applying the approach considered for
spatio-homogeneous regimes to every such group of the elements,
we obtain expressions for the parameter perturbations to convert the coupled
map chain (1) from the regime of spatiotemporal
chaos to the spatio-periodic structures mentioned above.
.
Then, using the system (10) and applying the approach considered for
spatio-homogeneous regimes to every such group of the elements,
we obtain expressions for the parameter perturbations to convert the coupled
map chain (1) from the regime of spatiotemporal
chaos to the spatio-periodic structures mentioned above.
For example, for the controlled transition to the state with ![]() and T=2 the following form of perturbations has been used:
and T=2 the following form of perturbations has been used:
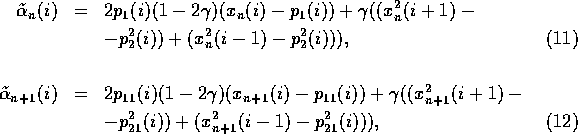
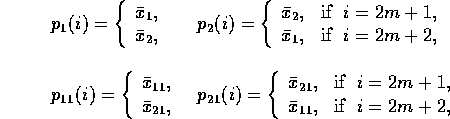
where ![]() are values of the
fixed points (see fig.1d),
are values of the
fixed points (see fig.1d), ![]()
To convert the lattice to the state with ![]() and T=2, the character
of the perturbations is as follows:
and T=2, the character
of the perturbations is as follows:
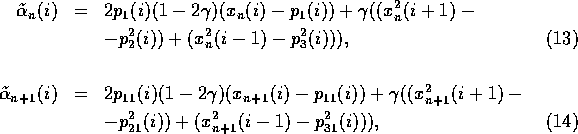
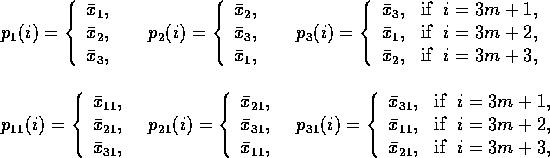
where ![]() are the values of the fixed points (see fig. 1e),
are the values of the fixed points (see fig. 1e),
![]()
Forms of the parameter perturbations to convert the system to the spatio-
periodic structure with ![]() and T=4 can be obtained in the
similar way.
The figure 1d-f demonstrates the results of numerical simulation for the
controlled transition from the spatiotemporal chaos to spatio-periodic
structure with
and T=4 can be obtained in the
similar way.
The figure 1d-f demonstrates the results of numerical simulation for the
controlled transition from the spatiotemporal chaos to spatio-periodic
structure with ![]() (fig. 1d),
(fig. 1d), ![]() (fig. 1e),
(fig. 1e),
![]() (fig. 1f).
In principle, the procedure of control is the same as in the case of
spatio-homogeneous states. Only the form of the parameter perturbations gets
complicated: the form of the chosen structure is more complicated, the
character of the perturbation is more complicated. It depends on both a
coordinate i and an iteration n, when a value of the dynamical
variable falls within the neighbourhood of the fixed point.
(fig. 1f).
In principle, the procedure of control is the same as in the case of
spatio-homogeneous states. Only the form of the parameter perturbations gets
complicated: the form of the chosen structure is more complicated, the
character of the perturbation is more complicated. It depends on both a
coordinate i and an iteration n, when a value of the dynamical
variable falls within the neighbourhood of the fixed point.
In considered situations if we use not all but a part of conditions on the parameter perturbations (11-14), the effect of control is reached also. However, in this case the time of transient process extremely grows.
Suggested approach for spatiotemporal chaos control can be applied to
chains with other kinds of coupling. It is easy to get expressions for the
parameter ![]() perturbations to convert system (2) to different
spatio-homogeneous and spatio-periodic regimes. For example, for controlled
transition to the spatio-homogeneous regime with temporal period T=1
the expression of the parameter perturbations is as follows:
perturbations to convert system (2) to different
spatio-homogeneous and spatio-periodic regimes. For example, for controlled
transition to the spatio-homogeneous regime with temporal period T=1
the expression of the parameter perturbations is as follows:
![]()
The parameter perturbations ensuring transition to the spatio-periodic
structure with ![]() and T=2 in the chain (2) are as follows:
and T=2 in the chain (2) are as follows:
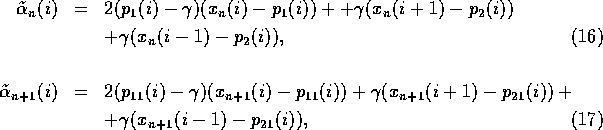
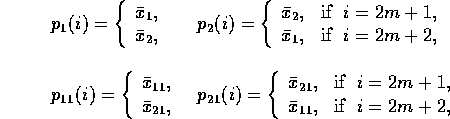
Numerical investigations have shown that spatiotemporal chaos in the linear coupled logistic map chain can be convert to the same spatio-homogeneous and spatio-periodic states which have been considered in system (1). The transient process of system (2) from the regime of spatiotemporal chaos to the chosen states does not differ qualitatively from the corresponding processes in system (1), which have been described and illustrated in fig. 1.
Efficiency of controlling chaos in the coupled map chains (1) and (2) depends
on magnitude of the parameter of nonlinearity ![]() and the coefficient
of coupling
and the coefficient
of coupling ![]() .
For example, preliminary investigations have shown that transformation
of system (1) to the spatio-homogeneous regime with temporal period one
in the interval of parameters values
.
For example, preliminary investigations have shown that transformation
of system (1) to the spatio-homogeneous regime with temporal period one
in the interval of parameters values ![]() and
and ![]() during 15000 iterations at N=20 is reached only in the range of the parameters
values allocated in the fig. 2 by hatching.
We could not transfer the system from chaotic regime to the spatio-homogeneous
one during 15000 iterations if
during 15000 iterations at N=20 is reached only in the range of the parameters
values allocated in the fig. 2 by hatching.
We could not transfer the system from chaotic regime to the spatio-homogeneous
one during 15000 iterations if ![]() was more than 0.04.
However, transition of the system to spatio-periodic regimes has been
feasible outside the allocated domain.
was more than 0.04.
However, transition of the system to spatio-periodic regimes has been
feasible outside the allocated domain.
It is evident that the possibility
to convert the system from the regime of spatiotemporal chaos to the desired
spatiotemporal structure depends on the probability of the chain element to
enter the ![]() -neighbourhood of the corresponding fixed point.
Fig. 3 demonstrates how the probability density of the existence of a chain
element variable
in the fixed point
-neighbourhood of the corresponding fixed point.
Fig. 3 demonstrates how the probability density of the existence of a chain
element variable
in the fixed point ![]() of the spatio-homogeneous
regime with T=1 depends on the parameter values. One can see that
the largest
magnitudes of the probability density are located in the domain, where the
controlled transition to the mentioned spatiotemporal state is observed
(see fig. 2).
of the spatio-homogeneous
regime with T=1 depends on the parameter values. One can see that
the largest
magnitudes of the probability density are located in the domain, where the
controlled transition to the mentioned spatiotemporal state is observed
(see fig. 2).
Both our preliminary investigations and the results of work (13) don't present comprehensive answer to the question about the dependence of the parameter values on the effect of chaos control. It requires further investigations.
CONTROL OF SPATIOTEMPORAL CHAOS IN TWO-DIMENSIONAL COUPLED MAP LATTICES
The suggested approach of controlling spatiotemporal chaos can be used to lattices of higher dimension.
Consider two-dimensional coupled logistic map lattice:
![]()
with periodic boundary conditions.
![]() is the size of the lattice).
is the size of the lattice).
When the parameters ![]() and
and ![]() are varied, complex spatiotemporal
dynamics is observed in the lattice. Without detailed discussion, we shall
only note that there exist parameters values areas with developed
spatiotemporal chaos. It is preceded by complicated bifurcational transitions
between different spatiotemporal regimes (16,17).
are varied, complex spatiotemporal
dynamics is observed in the lattice. Without detailed discussion, we shall
only note that there exist parameters values areas with developed
spatiotemporal chaos. It is preceded by complicated bifurcational transitions
between different spatiotemporal regimes (16,17).
To convert the lattice from the regime of spatiotemporal chaos
to regular states, we determine the form of the parameter perturbations
in the same way as for the chains.
As the example, we shall write the forms of perturbations for controlled
transition to spatio-homogeneous regimes with temporal
period T=s and to so-called "checkerboard structure" (17-19). In this structure
neighbouring elements of the lattice oscillate out-phase with temporal
period T=2. The prototype of this regime in the one-dimensional lattices
(1) and (2) is zigzag structure, which is spatio-periodic regime with
![]() and T=2.
and T=2.
From the analysis of the evolution equations of the dynamical variable perturbation of an element in the neighbourhood of the noted unstable regimes, it is seen that to convert the lattice (18) to the previously unstable spatio-homogeneous regimes with T=s we have to add the perturbation in the form:
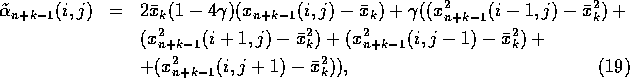
(where ![]() ,
, ![]() is the fixed point of the orbit with
T=s)
to the parameter of nonlinearity of the system.
is the fixed point of the orbit with
T=s)
to the parameter of nonlinearity of the system.
If the perturbation has the form:
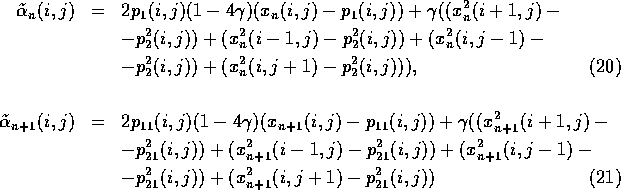

(where ![]() are the fixed points)
one can stabilize the checkerboard structure.
are the fixed points)
one can stabilize the checkerboard structure.
Figures 4-6 show the results of numerical simulation of spatiotemporal
chaos control in the two-dimensional coupled logistic map lattice.
The lattice with ![]() elements has been used in the experiments.
We have chosen the values of the parameters
elements has been used in the experiments.
We have chosen the values of the parameters ![]() and
and ![]() when there is
a regime of spatiotemporal chaos in the lattice (fig. 4a, 5a, 6a).
The procedure of control in the lattice have been the similar to that in the
chain. Following the value of the variable of every element
in the lattice we wait for the moment when it enters the chosen
when there is
a regime of spatiotemporal chaos in the lattice (fig. 4a, 5a, 6a).
The procedure of control in the lattice have been the similar to that in the
chain. Following the value of the variable of every element
in the lattice we wait for the moment when it enters the chosen
![]() -neighbourhood. Then, the corresponding perturbations of the system's
parameter are introduced if the conditions on the amplitude of the influence are
satisfied.
The figures consistently illustrate the controlled transitions from the
regime of spatiotemporal chaos to the spatio-homogeneous ones with T=1
(fig. 4), T=2 (fig. 5) and to the checkerboard structure (fig. 6).
-neighbourhood. Then, the corresponding perturbations of the system's
parameter are introduced if the conditions on the amplitude of the influence are
satisfied.
The figures consistently illustrate the controlled transitions from the
regime of spatiotemporal chaos to the spatio-homogeneous ones with T=1
(fig. 4), T=2 (fig. 5) and to the checkerboard structure (fig. 6).
The transient process is the same as in the chains. At first, there appear small randomly distributed patterns, expanding step-by-step and as the result occupying the whole lattice (see fig. 4-6).
CONCLUSIONS
This work presents a method of spatiotemporal chaos control in one- and two-dimensional coupled map lattices. The controlled transitions from the regime of spatiotemporal chaos to different chosen regular spatiotemporal states have been demonstrated following the example of the logistic map lattices with two kinds of coupling.
Duration of the transient process is rather small. Unfortunately, to apply this method it is necessary to know the obvious form of the dynamical system for determining structure of the available system parameter. Nevertheless, we suppose the obtained results can be useful for study of processes of spatiotemporal chaos control in more complicated lattices with unknown view of a partial element.
ACKNOWLEDGMENTS
The work was supported by International Science Foundation (grant RNO 000)
and Russian Foundation of Fundamental Natural Sciences (grant 93-8.2-10)