Lindenberg Katja

Nonclassical kinetics in constrained geometries:
initial condition and finite size effects
Katja Lindenberg
Department of Chemistry and Biochemistry
University of California, San Diego
La Jolla, CA 92093-0340, USA

Diffusion-limited reactions in low dimensions under a variety of conditions lead to the spontaneous formation of spatial patterns and to associated anomalous" rate laws for the global densities of the reacting species. For example, the irreversible reaction under normal" circumstances is described by the rate law whereas the actual asymptotic rate law for dimensions d;SPMlt;2 in an infinite volume is . The irreversible reaction under normal" circumstances is described by the rate law , where and are the global densities of the species A and B respectively. If , then the densities of the two species are equal at all times and we can dispense with the subscripts so that once again . The actual asymptotic rate law in an infinite volume in dimensions d;SPMlt;4 for an initially random distribution of reactants is .

Physically, the slow-down implied by the higher asymptotic exponents reflects a non-random spatial distribution of reactants. Consider, for example, the A+A reaction. A random or mixed" distribution of A's has a Hertz distribution of nearest neighbor distances, and this distribution in turn leads to the normal rate law. The salient characteristic of the Hertz distribution is its maximum at zero separation, indicative of the presence of many extremely close nearest neighbor pairs of reactant particles. An anomalous rate law implies a deviation from the Hertz distribution wherein there are many fewer close reactant pairs. Indeed, in dimensions lower than two an initially random distribution quickly settles into a distribution that peaks at a finite (nonzero) nearest neighbor separation, leading to an almost crystal-like average arrangement of reactants. This non-random distribution arises from the fact that diffusion is not an effective mixing mechanism in low dimensions.

In the A+B system the principal cause of the anomalous behavior is the formation of aggregates of like particles. The spatial regions in which the density of one type of particle is overwhelmingly greater than that of the other grow in time (while the total density within each aggregate of course decreases with time). Since the reaction can essentially only occur at the interfaces between aggregates, and since the number of these interfaces decreases with time, the reaction slows down relative to the rate that would describe a random mixture of reactants. Again, this behavior reflects the fact that diffusion is not an effective mixing mechanism in low dimensions. Note that initial spatial fluctuations in relative densities are essential for this ordering effect to occur: these fluctuations grow in size as the reaction that eliminates close opposite pairs proceeds.

The particular rate law is associated with a random initial distribution of reactants in an infinite volume. The situation changes with different initial fluctuations in the particle distribution and also with system geometry. Although initial fluctuations in general tend to grow in low dimensions and hence lead to anomalous behavior in the global rate laws, the specific exponent in the rate law differs for different initial distributions, as does the critical dimension for anomalous behavior. In particular, initial correlations tend to limit the fluctuations and hence the development of segregated patterns at later times. We thus see an example of an intriguing phenomenon wherein greater disorder initially leads to greater order at later times, and wherein the asymptotic behavior of a system forever reflects the initial conditions.

In this presentation we discuss the various regimes of kinetic behavior of the densities of reactants from the initial time until the asymptotic behavior is reached, and we do so for a variety of initial conditions and geometries.

Attracting cycles in bimodal piecewise linear maps
Yu.L. Maistrenko, V.L. Maistrenko and S.I. Vikul
Institute of Mathematics, National Academy of Sciences of Ukraine,
Kiev, Ukraine

We study the bifurcations in bimodal piecewise linear one-dimensional map

\

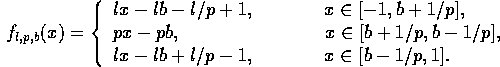
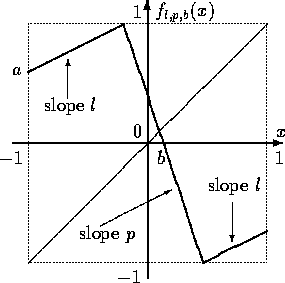
Let Then has the form of linear circle map. When, furthermore, l=1 we get a shift map with rotation number equal (1-b)/2. When l;SPMlt;1 the regions of synchronization (Arnold's tongues) arise: in each such region attracting cycle exists with rotation number r/q. This cycle is a global attractor for the map ; it has q-r points inside left-hand segment [-1,b] and r points inside right-hand segment [b,1]. Note, that all the regions are dense in the parameter rectangle defined by , .

The cycles can be classified by means of the notion of level of complexity according to "Farey tree". By recurrency, we obtain formulas for (k+1)-th complexity tongues in terms of the previous k-th complexity tongues, then, we extend these formulas for the range of parameter values and for different slopes and (taken at the left and right branches of , respectively).

At destruction of is always a result of so-called "border collision bifurcation", giving rise to the appearance of the cycle of nontrivial intervals (chaotic or not), but with the same rotation number r/q. Appeared interval cycle is attracting for ; length of its intervals being equal zero at the bifurcation moment, then grows continuously. Dynamics on is defined by a skew tent map (with slopes and correspondingly). Therefore after the bifurcation, attractor is either point cycle or cycle of chaotic intervals of the period mq (m can be any positive integer). Physical interpretation for this phenomenon may be as appearance of high subgarmonics, periodic or chaotic depending on parameters. Formulas for these bifurcations complete a general bifurcation picture for destructions of the regions of synchronization in the three-segment piecewise linear case.

Also, we study the bifurcation of the transition from skew tent map to bimodal map in parameter plane (l,p,b) occurring at b=1+1/p and b=1-1/p. It can result in the appearance of attracting cycles for periodics of which period adding sequence are observed. Typicalness of multistability phenomenon are shown: we find parameter regions where has two attracting point cycles as well as one attracting point cycle and one attracting cycle of chaotic intervals.