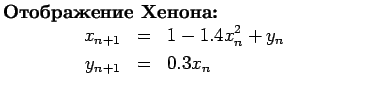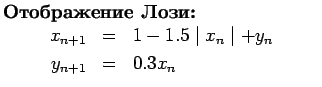практикума "Анализ временных рядов":
Фрактальные размерности
|
|
|
|
|
|
К настоящему времени разработаны различные методы, позволяющие проводить
численное исследование сложных режимов колебаний. С этой целью может
использоваться, например, спектральный анализ. Однако, расчет спектров не
дает возможности отличать хаотическую динамику в системах с малым числом
степеней свободы от динамики многомерных систем. Визуально очень похожие
спектры могут быть получены как для детерминированных хаотических колебаний,
так и для случайных процессов.
Определенные преимущества имеет исследование
траекторий в фазовом пространстве с помощью сечений Пуанкаре. Но при этом
удается получать только качественную информацию, причем, для наглядного
представления о геометрии анализируемых объектов размерность фазового
пространства не должна быть больше трех.
Образом хаотического режима колебаний в фазовом пространстве является
странный аттрактор - геометрически очень сложный объект. Особенности его
геометрии можно количественно охарактеризовать с помощью
фрактальных размерностей.
Существуют различные виды размерностей. Размерность фазового
пространства (![]() ) соответствует количеству переменных, определяющих
состояние динамической системы (ДС). Если математическая модель ДС задана
в виде системы обыкновенных дифференциальных уравнений первого порядка:
) соответствует количеству переменных, определяющих
состояние динамической системы (ДС). Если математическая модель ДС задана
в виде системы обыкновенных дифференциальных уравнений первого порядка:
| (1) |
Другое определение размерности было предложено Хаусдорфом. Пусть ![]() -
некоторое множество в пространстве
-
некоторое множество в пространстве ![]() . Предположим, что мы покрываем
данное множество кубиками
. Предположим, что мы покрываем
данное множество кубиками ![]() с величиной ребра, не превышающей
некоторое значение
с величиной ребра, не превышающей
некоторое значение ![]() . При этом каждая точка множества
. При этом каждая точка множества ![]() должна
обязательно попасть в тот или иной кубик. Тогда мера Хаусдорфа
должна
обязательно попасть в тот или иной кубик. Тогда мера Хаусдорфа
![]() вводится следующим образом:
вводится следующим образом:
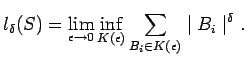 |
Здесь
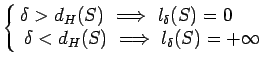 |
Согласно данному определению, ![]() может принимать нецелые значения.
В общем случае, если размерность является нецелой, ее называют фрактальной. Соответственно, объекты, характеризующиеся нецелой
размерностью, называют фракталами. Наличие нецелой размерности
является типичной особенностью хаотических аттракторов.
может принимать нецелые значения.
В общем случае, если размерность является нецелой, ее называют фрактальной. Соответственно, объекты, характеризующиеся нецелой
размерностью, называют фракталами. Наличие нецелой размерности
является типичной особенностью хаотических аттракторов.
Хотя понятие размерности Хаусдорфа хорошо определено с точки зрения математики, ее чрезвычайно сложно вычислить. Поэтому обычно используют более ``практичные'' определения фрактальных размерностей.
Одним из таких ``практичных'' определений размерности является емкость
(или емкостная размерность ![]() ). Пусть
). Пусть ![]() - некоторое множество в
пространстве
- некоторое множество в
пространстве ![]() , которое покрывается кубиками размера
, которое покрывается кубиками размера ![]() .
Если обозначить через
.
Если обозначить через ![]() число кубиков, необходимых для
покрытия всего множества, то емкость представляет собой предел следующего
вида:
число кубиков, необходимых для
покрытия всего множества, то емкость представляет собой предел следующего
вида:
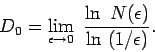 |
(2) |
По сути, эта величина характеризует, как меняется число элементов покрытия
при изменении ![]() :
:
Если в качестве ![]() рассматривается единственная точка, то
рассматривается единственная точка, то ![]() и не зависит от
и не зависит от ![]() :
:
Если анализируется отрезок линии (рис. 1) длины ![]() , то
, то
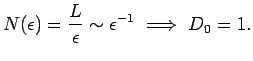 |
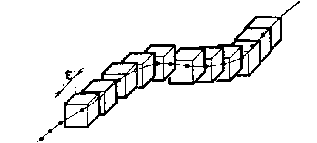
|
|
Рис. 1.
Покрытие отрезка линии кубиками размера |
Для поверхности площади ![]() :
:
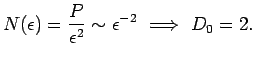 |
Во всех этих случаях емкость ![]() совпадает с топологической размерностью
совпадает с топологической размерностью
![]() и является целым числом. В качестве примера объекта с дробной
размерностью
и является целым числом. В качестве примера объекта с дробной
размерностью ![]() (т.е. фрактального объекта) рассмотрим Канторово
множество. Процедура его построения состоит в следующем. Берется отрезок
единичной длины [0, 1]; разбивается на 3 равные части, средняя из которых
выбрасывается. В результате, на первом шаге процедуры построения Канторова
множества мы получаем два отрезка [0, 1/3] и [2/3, 1] длины
(т.е. фрактального объекта) рассмотрим Канторово
множество. Процедура его построения состоит в следующем. Берется отрезок
единичной длины [0, 1]; разбивается на 3 равные части, средняя из которых
выбрасывается. В результате, на первом шаге процедуры построения Канторова
множества мы получаем два отрезка [0, 1/3] и [2/3, 1] длины ![]() (рис. 2). На следующем шаге каждый из этих отрезков вновь разбивается на 3
равные части, и опять выбрасывается средняя часть. Такая процедура
продолжается со всеми оставшимися отрезками. Если для покрытия множества на
некотором шаге k используются кубики с величиной ребра
(рис. 2). На следующем шаге каждый из этих отрезков вновь разбивается на 3
равные части, и опять выбрасывается средняя часть. Такая процедура
продолжается со всеми оставшимися отрезками. Если для покрытия множества на
некотором шаге k используются кубики с величиной ребра
![]() , то
необходимое количество кубиков составит
, то
необходимое количество кубиков составит
![]() .
.

|
| Рис. 2. Процедура построения Канторова множества. |
Таким образом:
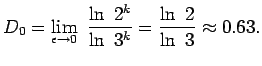 |
Если говорить о геометрии данного объекта, то Канторово множество есть нечто
большее, чем точка (для которой ![]() ), но нечто меньшее, чем интервал
(
), но нечто меньшее, чем интервал
(![]() ). Для Канторова множества емкость совпадает с размерностью
Хаусдорфа
). Для Канторова множества емкость совпадает с размерностью
Хаусдорфа ![]() , но не совпадает с топологической размерностью
(
, но не совпадает с топологической размерностью
(![]() ). В общем случае справедливо неравенство:
). В общем случае справедливо неравенство:
Еще одним примером фрактала служит объект, называемый ``снежинкой'' (либо кривой Кох). ``Снежинка'' имеет удивительное свойство: ее периметр является бесконечным, тогда как сама она занимает ограниченную площадь на плоскости. Процедура построения ``снежинки'' состоит в следующем. Рассматривается равносторонний треугольник, каждая сторона которого разбивается на 3 равные части, и к средней части ``пририсовывается'' равносторонний треугольник меньшего размера (рис. 3). Затем данная процедура повторяется с каждым отрезком полученной геометрической фигуры.
|
| Рис. 3. ``Снежинка''. |
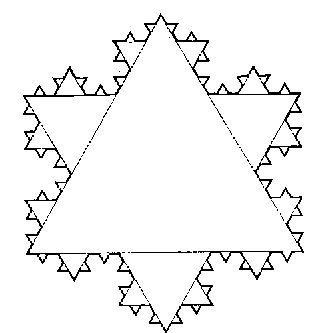
На рисунках 4-6 изображены еще несколько примеров процедуры построения фрактальных объектов. Для получения ``салфетки'' Серпинского (рис. 4) из черного равностороннего треугольника вырезается треугольник меньшего размера (с длиной стороны, уменьшенной в 2 раза); та же процедура осуществляется с каждым из вновь образованных треугольников. С ``салфеткой'' Серпинского тесно связан другой пример - ``ковер'' Серпинского. В отличие от рис. 4, в качестве исходного объекта выбирается квадрат, из которого вырезаются квадраты меньшего размера (рис. 5). Если осуществлять данную операцию бесконечное число раз (то есть осуществить переход к предельной фрактальной кривой), то черные участки исходного квадрата исчезают, а полный периметр ``дыр'' в ``ковре'' Серпинского становится бесконечным.
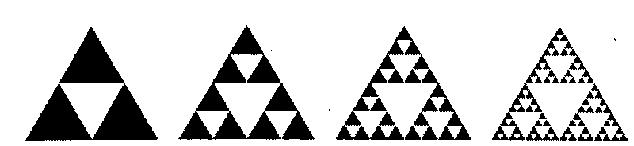
|
| Рис. 4. ``Салфетка'' Серпинского. |
|
| Рис. 5. ``Ковер'' Серпинского. |
На рис. 6 изображена процедура построения квадратной кривой Кох. В качестве
исходного объекта выбирается квадрат, каждая сторона которого заменяется
ломаной, состоящей из 8 отрезков равной длины. Во всех рассмотренных
примерах значение ![]() легко можно вычислить аналитически.
легко можно вычислить аналитически.

|
| Рис. 6. Квадратная кривая Кох. |
К сожалению, во многих случаях, представляющих практический интерес
(например, если мы будем анализировать сложную геометрию объектов фазового
пространства), вычислить емкость можно только численно (на компьютере); при
этом определение ![]() непосредственно по формуле (2) зачастую осложняется
очень медленной сходимостью отношения
непосредственно по формуле (2) зачастую осложняется
очень медленной сходимостью отношения
![]() к
пределу
к
пределу
![]() (если речь идет о расчете емкости объекта в
фазовом пространстве размерности
(если речь идет о расчете емкости объекта в
фазовом пространстве размерности ![]() , например, странного аттрактора).
Кроме того,
, например, странного аттрактора).
Кроме того, ![]() не зависит от вероятности посещения тех или иных областей
фазового пространства, т.е. не учитывает статистические свойства потока,
обусловленные динамикой системы (1). Поэтому на практике вместо емкости
предпочитают вычислять корреляционную размерность
не зависит от вероятности посещения тех или иных областей
фазового пространства, т.е. не учитывает статистические свойства потока,
обусловленные динамикой системы (1). Поэтому на практике вместо емкости
предпочитают вычислять корреляционную размерность ![]() , которую можно легче
(и быстрее) оценить численно. Для объектов с целой размерностью
, которую можно легче
(и быстрее) оценить численно. Для объектов с целой размерностью ![]() . В
более общем случае
. В
более общем случае ![]() .
.
Рассмотрим ДС вида (1), демонстрирующую хаотический режим колебаний.
Решением системы уравнений (1) является фазовая траектория ![]() . При
проведении численных исследований осуществляется анализ не непрерывных функций
времени, а дискретных значений
. При
проведении численных исследований осуществляется анализ не непрерывных функций
времени, а дискретных значений
![]() , где
, где ![]() - шаг
дискретизации (он может быть выбран равным, например, шагу интегрирования).
То есть, мы имеем дело с многомерными временными рядами
- шаг
дискретизации (он может быть выбран равным, например, шагу интегрирования).
То есть, мы имеем дело с многомерными временными рядами
![]() , где
, где ![]() - число точек анализируемых данных.
Предположим, что фазовая траектория
- число точек анализируемых данных.
Предположим, что фазовая траектория ![]()
![]() -мерной ДС (1) лежит на
некотором аттракторе A и возвращается в любую сколь угодно малую
окрестность произвольной точки данного аттрактора. В этом случае
корреляционную размерность
-мерной ДС (1) лежит на
некотором аттракторе A и возвращается в любую сколь угодно малую
окрестность произвольной точки данного аттрактора. В этом случае
корреляционную размерность ![]() можно вычислить по формуле:
можно вычислить по формуле:
| (3) |
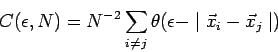 |
(4) |
Расчет корреляционной размерности может производиться непосредственно по
массиву векторов
![]() . Однако, для оценки
. Однако, для оценки ![]() аттрактора
A часто бывает более целесообразно осуществлять переход к сечению Пуанкаре и
вычислять корреляционную размерность точек в сечении (
аттрактора
A часто бывает более целесообразно осуществлять переход к сечению Пуанкаре и
вычислять корреляционную размерность точек в сечении (![]() ). Размерность
аттрактора A в этом случае определяется увеличением значения
). Размерность
аттрактора A в этом случае определяется увеличением значения ![]() на
единицу:
на
единицу:
![]() . Отметим одно важное обстоятельство: вычисление
. Отметим одно важное обстоятельство: вычисление
![]() позволяет получать некоторую оценку снизу значения емкости
позволяет получать некоторую оценку снизу значения емкости ![]() либо
размерности Хаусдорфа аттрактора A. Причем, если корреляционная
размерность рассматривается именно как оценка
либо
размерности Хаусдорфа аттрактора A. Причем, если корреляционная
размерность рассматривается именно как оценка ![]() , нужно принимать во
внимание, что
, нужно принимать во
внимание, что ![]() может существенно отличаться от размерности Хаусдорфа
(в частности, для хаотического аттрактора в системе Ресслера
может существенно отличаться от размерности Хаусдорфа
(в частности, для хаотического аттрактора в системе Ресслера ![]() может принимать
значение
может принимать
значение ![]() , тогда как
, тогда как ![]() ). В связи с этим расчеты
корреляционной размерности являются более привлекательными при исследовании
ДС по одномерным ``проекциям'' фазовой траектории (скалярным временным рядам).
В этом случае расчет корреляционной размерности позволяет сделать вывод о
наличии (либо отсутствии) маломерной динамики системы. Метод расчета
). В связи с этим расчеты
корреляционной размерности являются более привлекательными при исследовании
ДС по одномерным ``проекциям'' фазовой траектории (скалярным временным рядам).
В этом случае расчет корреляционной размерности позволяет сделать вывод о
наличии (либо отсутствии) маломерной динамики системы. Метод расчета ![]() по скалярному временному ряду имеет лишь небольшое отличие от рассмотренного
выше подхода: в формуле для корреляционного интеграла (4)
вместо массива векторов
по скалярному временному ряду имеет лишь небольшое отличие от рассмотренного
выше подхода: в формуле для корреляционного интеграла (4)
вместо массива векторов
![]() , который предполагается неизвестным, рассматривается
другой массив
, который предполагается неизвестным, рассматривается
другой массив
![]() , полученный в результате реконструкции
аттрактора A (задача реконструкции будет подробно рассмотрена в следующем
разделе). Сама процедура расчета корреляционного интеграла при этом не
меняется.
, полученный в результате реконструкции
аттрактора A (задача реконструкции будет подробно рассмотрена в следующем
разделе). Сама процедура расчета корреляционного интеграла при этом не
меняется.
Реконструкция представляет собой метод исследования динамических систем вида
(1) по временным зависимостям одной (или нескольких) переменных ![]() . Ранее
считалось, что для изучения динамики автоколебательной системы в терминах
фазового пространства необходимо знание всех координат, определяющих ее
состояние. Однако, в начале 80-х годов данное представление подверглось
пересмотру. Было обосновано, что фазовый портрет динамической системы (1)
может быть восстановлен по временному ряду
. Ранее
считалось, что для изучения динамики автоколебательной системы в терминах
фазового пространства необходимо знание всех координат, определяющих ее
состояние. Однако, в начале 80-х годов данное представление подверглось
пересмотру. Было обосновано, что фазовый портрет динамической системы (1)
может быть восстановлен по временному ряду ![]() (представляющему собой
дискретизованную с шагом
(представляющему собой
дискретизованную с шагом ![]() временную зависимость одной из
``наблюдаемых'' переменных ДС:
временную зависимость одной из
``наблюдаемых'' переменных ДС:
![]() ),
если в качестве недостающих координат вектора состояния используется тот же
самый ряд
),
если в качестве недостающих координат вектора состояния используется тот же
самый ряд ![]() , взятый с некоторым запаздыванием. В 1981г. Такенсом была
доказана теорема, утверждавшая следующее: Предположим, что фазовая
траектория
, взятый с некоторым запаздыванием. В 1981г. Такенсом была
доказана теорема, утверждавшая следующее: Предположим, что фазовая
траектория ![]() некоторой
некоторой ![]() мерной ДС (1) лежит на аттракторе
мерной ДС (1) лежит на аттракторе ![]() ,
принадлежащем гладкому
,
принадлежащем гладкому ![]() мерному многообразию.
Тогда по одномерной ``проекции''
мерному многообразию.
Тогда по одномерной ``проекции'' ![]() этой траектории методом задержки (5)
можно получить
этой траектории методом задержки (5)
можно получить ![]() мерную реконструкцию
мерную реконструкцию ![]() исходного аттрактора
исходного аттрактора ![]() как
множество векторов
как
множество векторов ![]() в
в ![]() при
при ![]() :
:
| (5) |
Согласно теореме Такенса, отображение
![]() является гладким и обратимым на
является гладким и обратимым на ![]() почти для любого
почти для любого ![]() (если
(если
![]() ). Это означает, что
множество восстановленных
). Это означает, что
множество восстановленных ![]() -векторов может быть обработано вместо
исходных (и часто неизвестных нам) векторов
-векторов может быть обработано вместо
исходных (и часто неизвестных нам) векторов ![]() с целью вычисления
метрических (фрактальные размерности) или динамических (ляпуновские
показатели) характеристик аттрактора
с целью вычисления
метрических (фрактальные размерности) или динамических (ляпуновские
показатели) характеристик аттрактора ![]() системы (1).
системы (1).
В действительности, на компьютере анализируется ряд значений переменной
![]() в дискретные моменты времени
в дискретные моменты времени ![]() , поэтому реконструируемое
множество векторов также является дискретным
, поэтому реконструируемое
множество векторов также является дискретным
![]() , а
величина
, а
величина ![]() , называемая задержкой, имеет вид
, называемая задержкой, имеет вид
![]() ,
где
,
где ![]() - целое число. Иными словами, на практике равенство (5) может быть
переписано следующим образом:
- целое число. Иными словами, на практике равенство (5) может быть
переписано следующим образом:
где нижний индекс
Сама техника реконструирования состоит в выборе значений задержки ![]() ,
размерности пространства вложения
,
размерности пространства вложения ![]() и в формировании массива векторов
и в формировании массива векторов
![]() . Предполагается, что полное время наблюдения
. Предполагается, что полное время наблюдения
![]() и число точек
и число точек ![]() достаточно велики, чтобы по
траектории можно было судить о важнейших свойствах интересующего нас
аттрактора.
достаточно велики, чтобы по
траектории можно было судить о важнейших свойствах интересующего нас
аттрактора.
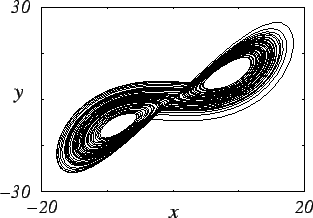
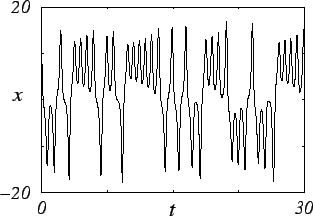
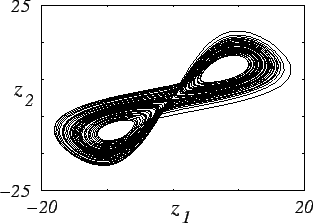
В качестве примера рассмотрим уравнения модели Лоренца:
| (6) | |||
при значениях параметров
|
| (а) |
|
| (б) |
|
| (в) |
|
Рис. 7. Проекция фазового портрета хаотического
аттрактора системы Лоренца (а), временная зависимость координаты |
На практике мы всегда работаем с конечным числом точек
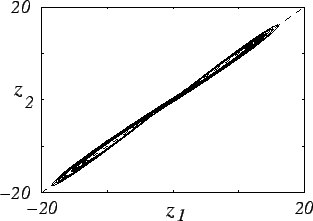
|
| (а) |
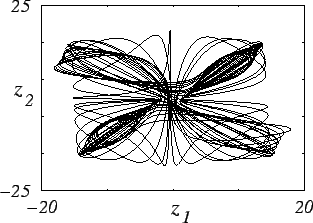
|
| (б) |
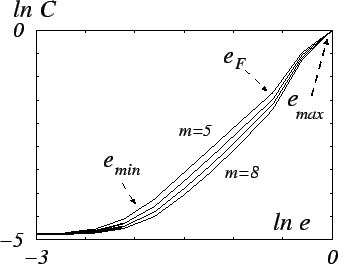
|
|
Рис. 9. Графики зависимостей
|
Для удобства анализа вместо зависимости
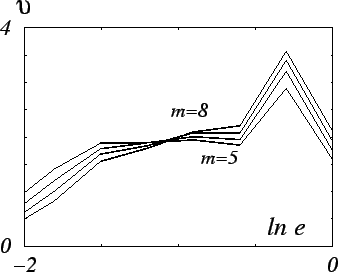
|
| Рис. 10. Графики локальных наклонов. |
Точность определения размерности определяется длиной линейного участка, т.е. величиной
При работе с временными рядами обычно поступают следующим образом. Выбирают
произвольное (малое) значение размерности пространства вложения ![]() и
вычисляют
и
вычисляют ![]() по наклону линейного участка графика
по наклону линейного участка графика
![]() от
от
![]() . Затем увеличивают
. Затем увеличивают ![]() на единицу и вновь определяют
на единицу и вновь определяют ![]() .
Таким образом, анализируется зависимость результатов расчета корреляционной
размерности от выбора пространства вложения. Данный прием позволяет сделать
вывод о наличии (либо отсутствии) маломерной динамики: при ее наличии
зависимость
.
Таким образом, анализируется зависимость результатов расчета корреляционной
размерности от выбора пространства вложения. Данный прием позволяет сделать
вывод о наличии (либо отсутствии) маломерной динамики: при ее наличии
зависимость ![]() быстро достигает насыщения (например,
быстро достигает насыщения (например, ![]() ) и при
дальнейшем увеличении
) и при
дальнейшем увеличении ![]() не меняется (в пределах точности вычисления). Если
маломерная динамика отсутствует, то
не меняется (в пределах точности вычисления). Если
маломерная динамика отсутствует, то ![]() увеличивается с ростом
увеличивается с ростом ![]() . В этом
случае при достаточно больших
. В этом
случае при достаточно больших ![]() возможно насыщение, которое обусловлено
фундаментальными ограничениями на значение корреляционной размерности,
связанными с конечной длиной анализируемого временного ряда:
возможно насыщение, которое обусловлено
фундаментальными ограничениями на значение корреляционной размерности,
связанными с конечной длиной анализируемого временного ряда:
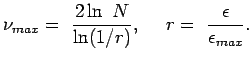 |
Данная формула означает, что алгоритм расчета размерности не может дать значение больше, чем
Практическая реализация алгоритма расчета размерности ![]() предполагает
составление программы вычисления корреляционного интеграла в широком
диапазоне по параметру
предполагает
составление программы вычисления корреляционного интеграла в широком
диапазоне по параметру ![]() и нахождение локальных наклонов
зависимости
и нахождение локальных наклонов
зависимости
![]() от
от ![]() . Если уравнения ДС (1)
известны, т.е. мы можем проинтегрировать математическую модель, в формуле
(4) рассматривается массив векторов
. Если уравнения ДС (1)
известны, т.е. мы можем проинтегрировать математическую модель, в формуле
(4) рассматривается массив векторов ![]() . При работе с одномерным
временным рядом предварительно проводится реконструкция (выбирается значение
задержки и размерности пространства вложения), после чего в формуле (4)
рассматривается массив векторов
. При работе с одномерным
временным рядом предварительно проводится реконструкция (выбирается значение
задержки и размерности пространства вложения), после чего в формуле (4)
рассматривается массив векторов ![]() . При расчете
. При расчете ![]() можно
выделить 3 важные характеристики массива данных: полное время наблюдения
можно
выделить 3 важные характеристики массива данных: полное время наблюдения
![]() , число точек
, число точек ![]() и шаг между ними
и шаг между ними ![]() . Они связаны
соотношением
. Они связаны
соотношением
![]() . Их следует рассматривать вместе,
поскольку одного из них недостаточно: большое
. Их следует рассматривать вместе,
поскольку одного из них недостаточно: большое ![]() при малом
при малом ![]() может
быть столь же плохо как и малое
может
быть столь же плохо как и малое ![]() при большом
при большом ![]() . Очевидно,
например, что размерность
. Очевидно,
например, что размерность ![]() аттрактора не может быть вычислена, если в
малые окрестности точек в фазовом пространстве будет попадать меньше
аттрактора не может быть вычислена, если в
малые окрестности точек в фазовом пространстве будет попадать меньше ![]() соседей. Если расчет размерности сопровождается процедурой реконструкции
аттрактора, появляются дополнительные параметры, которые также влияют на
точность расчетов. Для того, чтобы быть уверенным в результатах вычислений,
экспериментаторы предпочитают немного ``покрутить'' различные параметры и
убедиться, что полученные оценки
соседей. Если расчет размерности сопровождается процедурой реконструкции
аттрактора, появляются дополнительные параметры, которые также влияют на
точность расчетов. Для того, чтобы быть уверенным в результатах вычислений,
экспериментаторы предпочитают немного ``покрутить'' различные параметры и
убедиться, что полученные оценки ![]() при этом будут меняться
незначительно.
при этом будут меняться
незначительно.
Меньше проблем возникает при исследовании дискретных отображений вида:
поскольку в этом случае уменьшается число параметров, от которых зависит точность определения корреляционной размерности (в частности, отсутствует
![]() Как написать, откомпиллировать и запустить простую С-программу
Как написать, откомпиллировать и запустить простую С-программу
![]() Как выводить результаты расчета на экран в виде графиков
Как выводить результаты расчета на экран в виде графиков
![]() Руководство по языку C
Руководство по языку C
![]() Использование программы gnuplot для оперативного вывода
графической информации.
Использование программы gnuplot для оперативного вывода
графической информации.
1) Ознакомление с теоретическим материалом.
2) Аналитический расчет размерности тестового примера
(указанный преподавателем вариант задания 1).
3) Написание программы реконструкции фазового портрета по предоставленной
одномерной реализации.
4) Экспериментальная оценка оптимальный временной задержки
(указанный преподавателем вариант задания 2).
5) Написание программы итерирования двумерных отображений (Хенона или
Лози).
6) Расчет корреляционной размерности хаотического аттрактора
(указанный преподавателем вариант задания 3).
7) Оформление отчета по полученным результатам.
Отчет по лабораторной работе представляется в виде latex или html документа по указанию преподавателя. Он должен содержать:
1) Заголовок, с указанием названия лабораторной работы, Ф.И.О. выполнявших ее студентов, номер учебной группы, номер задания.
2) Сведения (уравнения и комментарий) о модельной системе, смысл параметров, диапазон их изменения.
3) Построенную двупараметрическую бифуркационную диаграмму.
4) Информацию о количестве и типе аттракторов либо особых точек/траекторий в исследованной области и о смысле бифуркационных линий
5) Наброски фазовых портретов либо копии экрана, характеризующие поведение исследуемой системы в различных областях управляющих параметров.
6) Краткое резюме - заключение по пунктам 1-5.
Задание 1. Вычислить аналитически емкостную размерность:
(а) ``снежинки'' (рис. 3);
(б) Канторова множества (рис. 2), если при его построении проводится
разбиение отрезка [0, 1] не на 3 части, а на 5 (по-прежнему,
выбрасывается только одна - средняя часть);
(в) ``салфетки'' Серпинского (рис. 4);
(г) ``ковра'' Серпинского (рис. 5);
(д) квадратной кривой Кох (рис. 6).
Задание 2.
Составить программу реконструкции фазового портрета по предоставленному
временному ряду ![]() . Подбором задержки оценить оптимальное значение
временной задержки (исходя из геометрии реконструированного множества -
аттрактор не должен быть слишком вытянут ни в одном из направлений).
. Подбором задержки оценить оптимальное значение
временной задержки (исходя из геометрии реконструированного множества -
аттрактор не должен быть слишком вытянут ни в одном из направлений).
| N варианта | динамическая система | примечание |
| 1 | система Ресслера | N=3000,
|
| 2 | система Лоренца | N=3000,
|
| 3 | генератор с инерционной нелинейностью | N=3000,
|
| 4 | модель нефрона | N=3000,
|
| 5 | модель нейрона (Хиндмарш-Розе) | N=3000,
|
| 6 | модель бета-клетки | N=3000,
|
Задание 3.
Вариант (а):
Написать программу итерирования отображения Хенона,
которая будет записывать в файл с названием ``data'' в две колонки
соответственно значения ![]() ,
, ![]() . Число точек для расчета
. Число точек для расчета ![]() выбрать равным
выбрать равным ![]() . Вычислить корреляционную размерность хаотического
аттрактора в отображении Хенона с помощью программы ``cordim.x'', которая
считывает данные из файла ``data'' и выводит результаты расчета в
файл ``dim-out'' (в первую колонку данного файла записывается
. Вычислить корреляционную размерность хаотического
аттрактора в отображении Хенона с помощью программы ``cordim.x'', которая
считывает данные из файла ``data'' и выводит результаты расчета в
файл ``dim-out'' (в первую колонку данного файла записывается ![]() ,
во вторую
,
во вторую
![]() ). Оценить величину
). Оценить величину ![]() по наклону
линейного участка полученной зависимости.
по наклону
линейного участка полученной зависимости.
Вариант (б):
Определить корреляционную размерность хаотического аттрактора
в двумерной дискретной динамической системе Лози. С этой целью необходимо
выполнить те же операции, что и в варианте (а), только теперь в файл
``data'' будут записаны значения ![]() ,
, ![]() другой модельной системы.
другой модельной системы.
Вариант (в):
Определить корреляционную размерность хаотического
аттрактора в отображении Хенона по одной координате.
Для этого нужно записать в файл ``data'' в две колонки значения
![]() ,
, ![]() ,
,
![]() . Далее воспользоваться
программой ``cordim.x'' по аналогии с заданием 3(а).
. Далее воспользоваться
программой ``cordim.x'' по аналогии с заданием 3(а).
Вариант (г):
Определить корреляционную размерность хаотического аттрактора в
отображении Лози (8) по одной координате. Для этого нужно записать в
файл ``data'' в две колонки значения ![]() ,
, ![]() ,
,
![]() .
Далее воспользоваться программой ``cordim.x'' по аналогии с заданием 3(а).
.
Далее воспользоваться программой ``cordim.x'' по аналогии с заданием 3(а).